Figure 3.13
Fragments, p. 33 (redrawn).
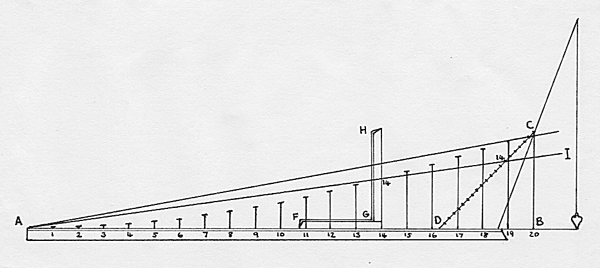
A full-scale technique for ‘circular’ lines. Although intended for general use, Baker explains his device by means of just a single example, the rising of the floor aft. As regards other applications: ‘What excellent things may be wrought by this in shipping I do leave unwritten in particular to the industrious mechanical.’
In the figure A is the beginning of the rising of the floor aft. In this ship there are 20 frames between A and C (the tuck). To find the height of the floor at each frame, CD is set up, with BD = BC. CD is then divided into as many equal parts as there are frames. With a line AI fixed at A and pulled taut, the height at any frame N is found by adjusting AI until it passes through the Nth point on CD. This height is then marked on the ‘square’ FGH.
Despite Baker’s claims to the contrary, the resulting curve is not circular; rather, it is part of an hyperbola, being represented by the equation y = x2/(x + k), where k = (AB/AC)(AB - AC) and A is taken as the origin of a Cartesian x-y coordinate system. To change the shape of the curve slightly, Baker recommends making CD more upright so that BD < BC. The curve remains hyperbolic except for the extreme case where D coincides with B, when it becomes parabolic.
Return to thesis chapter text.