Chapter 3
MATHEW BAKER AND THE ART OF THE SHIPWRIGHT
1. ‘FRAGMENTS OF ANCIENT ENGLISH SHIPWRIGHTRY’
From the gentleman Thomas Digges, the focus now turns to an older contemporary, Mathew Baker. Baker (c.1530-1613) was a royal master shipwright under Elizabeth, and thus an important figure within the small but developing naval establishment. With one and sometimes two senior colleagues, he was responsible for constructing or rebuilding many of the ships which tackled the Spanish Armada of 1588. In 1605, his standing at the head of the ‘Art or Mystery of building and making of Ships’ was confirmed when he was created first Master of the newly founded Company of Shipwrights.1
At first sight, the shift from Digges to Baker is a major one, without obvious points of contact. Apparently, we here move from the histories of science and mathematics, as represented by Digges’s geometry, astronomy and ballistics, to the history of technology. We also seem to make a parallel social transition from a self- [page 108:] conscious gentleman to the dockyard world of an artisan. Yet I shall suggest that these oppositions are overly stark. There are continuities between the work and identities of Digges and Baker, continuities which were established through the practice of mathematics and the creation of the mathematical practitioner.
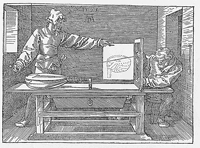
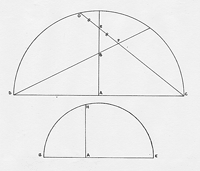
The starting point and emblem for this chapter is an image from a manuscript begun by Mathew Baker and known as Fragments of Ancient English Shipwrightry (Figure 3.1).2 The picture shows a master shipwright and an assistant at work in a drawing office, the master wielding giant-sized dividers over a ‘plat’ of a ship in plan and section. The image is extraordinarily rich and provides vital clues to Baker’s transformation of ship design into a mathematical art and his simultaneous self-fashioning as a mathematical practitioner.
Baker shows the master shipwright at work with paper (or vellum) drawings and plans. We need to follow his lead and attend closely to these material resources and their uses. Yet, though design is as important a category to the history of technology as experiment is to the history of science, the practice of paper-based design is so familiar as to be frequently taken for granted. Baker transports us back to a period when the design of ships was first being worked out on paper; his Fragments undercut the air of self-evidence which too often surrounds the practice of paper design. Rather than the wood of the ships themselves, it is therefore paper that [page 109: Figure 3.1] [page 110:] stands at the central focus of this study.3
Most importantly, it was precisely on paper that Baker could connect mathematics and ship design. By drawing and manipulating ships in the medium used to solve geometrical problems and perform arithmetical calculation, he was able to juxtapose previously unrelated domains. On paper, the problems and tasks of ship design could be posed in new terms, and techniques could be transferred, explored and adapted. Moreover, paper could circulate through and beyond the shipyard, reaching and speaking the language of those with no direct experience of shipyard life. Paper was a mobile ‘place’ where shipwright and mathematician could meet and exchange. Indeed, without paper, Baker’s mathematics and his contacts with mathematical practitioners would have been not just difficult but incomprehensible and impossible.
Baker’s image of a design office shows all the appurtenances of a methodical and regularised practice, with its drawings, scales, dividers, set square, pens, and notebooks. Yet this is not a transparent window onto the past, providing us with unmediated access to Baker’s workplace and procedures. It is itself a representation and was carefully constructed to communicate the image and values of the mathematising shipwright. Take the simple perspective scheme as an example. Despite their 15th-century Italian origins, the rules for perspective drawings remained novel in 16th century England and their results still carried a vivid sense of the powers of geometry. Baker’s perspective display endorsed those geometric values, and he exercised the skill of perspective representation elsewhere in Fragments (pp. 2-3). [page 111:]
However, aside from its use of perspective, the artifice of Baker’s drawing can be more radically dismantled. Figure 3.2 shows a room with two men creating a perspective image, and might seem a possible source for Baker’s general motif. A closer comparison, looking not at the human figures but at the table on which they are working, shows that the connection is much stronger: Baker’s table is a direct copy from the engraving. This exact source is the final woodcut in Albrecht Dürer’s Underweysung der Messung (1525), a heavily-illustrated treatise on practical geometry directed specifically at painters. As will become clear later, there is independent evidence elsewhere in Baker’s Fragments that he knew and borrowed from Dürer’s text. But the point here is that Baker was deliberately and self-consciously assembling his identity as a shipwright and designer, pulling together elements from the prestigious artistry and mathematics of Dürer.
Now, the medium for Thomas Digges’s self-fashioning was the word. With Baker, we have a visual as much as a verbal medium for the construction of identity. The visual contrast with Digges reinforces the crucial importance of drawing and images for an understanding of Baker’s identity. Design is the primary context for his mathematical work.
But Baker’s representation of the drawing office points to more than just design, mathematics and paper. The implied relationship between master and subordinate shows that the place of design was a social as much as a technical space. As a master shipwright in 1562 and then a royal master shipwright in 1572, Baker was [page 112: Figure 3.2] [page 113:] accustomed to the exercise of control and managerial responsibility.4 Indeed, he had been brought up to occupy a privileged position within the trade, for his father, James Baker, had been a master shipwright to Henry VIII.5 The first surviving reference to Mathew is in a 1544 list of shipwrights in which, rather than appearing towards the end where his youth and low pay would have otherwise consigned him, he features at the top, directly under the name of his father.6 Though the Bakers did not create a dockyard dynasty comparable to that of the Pett family throughout the 16th and 17th centuries, Mathew Baker was clearly brought up to expect leadership and a place apart from ordinary workmen.7
As an elite shipwright, Baker’s status as a craftsman needs to be carefully and explicitly weighed. Unfortunately, in the existing historiography of scholars and craftsmen there is disturbingly little precision in pinning down the identity of artisans. Frequently there seems to be a tacit understanding that the craft world was made up of small workshops populated by individual masters, with perhaps an apprentice or two, and a journeyman. This stereotype is entirely inadequate for Baker.
Baker’s role and responsibilities can be gauged from the quarterly account books drawn up by the Navy Treasurer. Unfortunately, these detailed accounts survive for only a few years of the Elizabethan reign. However, the review of even a single year provides a good sense of Baker’s official status. [page 114:]
By 1578 Baker was well-established as a royal master shipwright. He began the year directing routine maintenance on the fleet stationed in Gillingham Water (Chatham) and was responsible for surveying the condition of the ships there.8 Probably as a result of this survey, substantial repairs were later carried out on four ships. Prior to the arrival of these decayed ships at Deptford, Baker supervised the construction and fitting of wooden ways in the dry dock, and it was probably also at this time that he and Peter Pett installed a new pair of floodgates at the head of the great dock there, ‘for the Speedier Receiving in and taking out of her graces ship Dry Docked and Repaired there.’
For the ship repairs themselves, Baker headed a workforce of shipwrights and caulkers at Deptford which runs to nine pages in the accounts. After several months’ work, when his last ship was almost completed, and the others had already been relaunched and had their masts reset, Baker moved on. An additional decayed ship arrived at Deptford for dismasting and was then taken to Woolwich to be dry-docked; Baker directed both the repair of the hull at Woolwich and the refashioning of the mast at Deptford. With this work over, he ended the year on a smaller-scale project at Woolwich, where he led a team of six shipwrights who broke down an old ship and then used the timber to frame a lighter for the transport of artillery.
Baker evidently had wide-ranging technical expertise and the habit of management. Moreover, he was not restricted to the royal shipyards. When a new [page 115:] ship was to be built it was common practice for the master shipwrights to go into the woods and mark the trees whose shapes and sizes were most appropriate for the projected vessel.9 Nor was Baker exclusively concerned with the building and maintenance of naval ships and dockyard structures. Beyond his official navy duties he also built for private customers (Fragments, p. 22 refers to the Edward of a ‘Mr Willames’). Baker’s entrepreneurial activity extended in other directions too. In 1578 he was paid for supplying materials to the navy and he also provided victuals and lodgings for shipwrights prested into royal service at both Woolwich and Deptford.
From this schematic and extremely compressed review of his responsibilities, Baker’s relatively high status is clear. Although the division of labour among the few permanent and many temporary naval workers was strongly developed, the masters had to display competence in diverse fields, and they were rewarded with position and pay at the top of the dockyard hierarchy. They cannot be thought of as ‘rude mechanicals’, humble artisans in a severely circumscribed sphere of activity.10 Rather, they were versatile figures who, with increasing seniority, were expected to manage resources and workers as well as direct the construction and repair of ships.
Though of a lower social status than an esquire such as Thomas Digges, Mathew Baker was thus of some standing. Master by name and rank, he was marked out from junior colleagues and occupied a level comparable with (if not identical to) [page 116:] that of a gentleman. Baker confounds the traditional category of the craftsman or artisan: he was working as a manager and technical leader, exercising responsibility in a strategic industry. Nor was shipping a static technology. All aspects of the industry were undergoing rapid development throughout Europe in the 15th and 16th centuries. Commercially, there were the early voyages of discovery and the subsequent development of long-distance trade. Organisationally, there was the establishment of the first permanent, ocean-going navies. Technically, there were challenges such as the adoption of Mediterranean carvel construction techniques in Northern Europe and the development of 3- and 4-masted full-rigged ships. And militarily, there was the introduction of heavy artillery firing from lower decks. The elevated role of the master shipwright needs to be understood in terms of these economic, administrative, technological and military changes.11
With its division of labour and stratification of management and control, the naval dockyard was already on its way to becoming a - if not the - major industrial site of the early modern world. Baker was at the heart of this capital-intensive industry. Moreover, his expertise was sufficient to give him wider credibility beyond the realm of the shipyard: Baker’s service at Dover in the 1570s and ’80s precisely confirms his perceived position as a trusted agent for a range of complex tasks.
Baker thus has an exemplary significance not just for shipbuilding and ship design but for larger questions in the history of technology and design. Traditionally, the study of technological design in the Renaissance has been devoted to civil and military architecture and the design of machines, with shipbuilding kept separate in the [page 117:] distinct domain of maritime history.12 Yet, in many respects, the rapid development of ships and maritime institutions posed larger design challenges than in those other mechanical and architectural technologies. The Venetian Vettor Fausto commented in 1530 that
if knowledge of the architecture of buildings on land is so thoroughly difficult, what should I say about that of the sea, where everything is drawn out not by straight lines (which is an almost easy method) but by curves and variations repeatedly made to them?13
Baker’s Fragments provide some of the most valuable archival evidence for these complex procedures of ship design. Moreover, they not only signal the extension of design into paper practice, but witness the new identity of the elite mechanician as mathematical practitioner.
2. THE PLACE OF DESIGN
Mathew Baker’s manuscript was christened Fragments of Ancient English Shipwrightry when it was acquired and preserved by Samuel Pepys. Pepys’s choice of title was deliberate and appropriate. Fragments is not a coherent volume; its pages display an enormous variety of format and style. Some parts are finely executed, perhaps for a planned presentation volume, while other sections are no more than notebook pages. There are coloured draughts of ships with their full decoration; [page 118:] historical and mythological sketches; a map; plans, elevations and sections of ships; and practical mathematical devices for scaling and generating proportions. Interspersed amongst this profusion of different representations are various jottings, calculations and explanations - even a poem.
The diversity of material in Fragments complicates the question of its dating. Though the volume illustrates and records details of ships built by Baker between the early 1570s and the mid-1580s, it is possible that the surviving text and images were drawn up in later years. Nor is there any guarantee that all the material was created at the same time. There is thus no secure way of linking Fragments to a particular stage of Baker’s long career. Unfortunately, aside from administrative records, which do not speak with Baker’s own voice, there are no other substantial sources for his design practice. Thus, in contrast to the case of Thomas Digges, it is not possible to reconstruct the development of Baker’s career and to investigate changes in his commitments, values and self-presentation. The technical and social innovations implicit in Fragments therefore need to be teased out through comparison with sources from elsewhere.
Though Fragments is one of the first and most important texts on shipbuilding, it is not the earliest to survive. From in and around the Venetian Arsenal, there exists a series of manuscripts which reach back as far as the early 15th century. These texts are cryptic in the extreme, using obscure local terminology to record the proportions of vessels, and accompanying their recipe-style instructions with rough sketches.14 Contemporary with Baker are the first surviving texts from [page 119:] the Iberian tradition (itself closely related to Italian practices). The most important texts were compiled by observers of shipbuilding rather than shipwrights and contrast markedly with the earlier Venetian documents. As educated outsiders, these Spanish and Portuguese authors brought the resources of literate culture to bear on their new subject. Drawing on classical precedents and literary forms, they produced discursive and systematic treatments of shipbuilding accessible to an audience unfamiliar with dockyard culture.15
Baker’s Fragments is distinct from both the Venetian and Iberian documents: his volume is not only the work of a practising shipwright but it incorporates innovative uses of paper such as his production of detailed and finely finished scale drawings. Indeed, the other European sources are, paradoxically, often more indicative of the design practice that preceded paper techniques.
So how were ships designed without paper? By the 16th century an apparatus of simple though powerful rules and techniques had been developed for large vessels. Ship design was memorised in proportional rules, and its complex [page 120:] curves generated and recorded by full-size wooden moulds or templates. Technically advanced shipwrights employed a sophisticated constructive geometry which used wood rather than paper and took place not in a design office but out in the shipyard itself.16
In the later 16th century, English naval vessels, like earlier Mediterranean and Iberian ships, were carvel or skeleton-built; that is, the keel was laid down, the stem and sternposts erected, and then the frames or ribs set up along the length of the keel, before the planking was applied. The shape of skeleton-built frames thus determined the form of the hull.17
However, carvel was (and is) a broad category, encompassing numerous solutions to the problem of moulding the timbers.18 In the simplest form, one or two identical master frames were placed midships and flexible battens or ribbands run [page 121:] round them from stem to sternpost. The shapes of all the other frames were then taken from the ribbands. The only frame actually to be specified in advance was the master frame, for the ribbands were adjusted during framing to give a fair form. More advanced techniques for large vessels reduced the reliance on ribbands, by pre-specifying the frames in the central section of the hull and reserving the use of ribbands to the ends of the ship, where the curves become sharper. The sophisticated techniques for deriving these pre-determined frames show the Renaissance shipwrights’ constructive geometry at work.
The shipwrights’ first step was to determine the form of the midship frame, since it was from this frame that the others in the central section of a ship were shaped. Proportional rules of thumb defined its dimensions and arcs, and its shape was recorded in the form of full-size templates (or moulds). Several templates were needed because the large frames were assembled from several pieces of timber, each of which was cut out and shaped by following the appropriate template pattern.
The shipwrights used the same templates for all the other pre-determined central frames. To generate the smoothly varying shape of the hull, the trick was to manipulate and reconfigure the relative orientations of these templates. Starting from the form of the midship frame, the templates were slightly adjusted for each of the other frames in the central section of the hull, in order to create the rising and narrowing of the ship’s lines towards bow and stern. These slight changes were controlled not by paper drawings or calculations but by full-scale graduations marked directly on the templates themselves, or on boards.
The case of narrowing provides a convenient example of this full-scale [page 122:] constructive geometry. Though mentioned in Venetian sources, the narrowing procedure was most clearly spelled out in the 16th century by one of the educated observers of the shipwright’s art, the Portuguese Fernando Oliveira.19
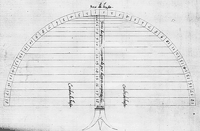
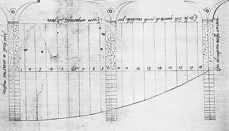
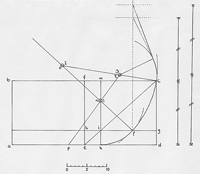
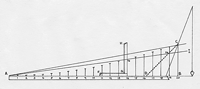
The shipwright used a proportional rule of thumb to calculate by how much the ship’s side should narrow between the midship frame and the tail-frame, the last frame fore or aft in the hull’s central section. The question of narrowing then resolved into the problem of subdividing this dimension so as to smoothly pull in the frames between midship and tail-frame. The narrowing dimension was first taken as a radius and used to produce a semicircle. On each quadrant the shipwright stepped out with dividers the same number of equal arcs as there were narrowing frames. Joining up the matching points gave a series of chords (Figure 3.3). The intersections of chord and radius produced a graduated scale that would then be used to smoothly narrow the hull (Figure 3.4). Each mark on the scale indicated the incremental amount by which successive frames were to be pulled in to narrow the hull: initially a small amount, but gradually more and more (Figure 3.5).
Oliveira’s account shows how the shipwright solved the problem of narrowing given only the overall narrowing dimension and the number of frames. However, while he usefully indicates the steps in the procedure, it needs to be emphasised that Oliveira’s text and drawings are in one sense fundamentally misleading. Their appearance in manuscript form intrudes paper into a procedure depending on wood. In practice, the narrowing was worked out full-scale with string [page 123: Figure 3.3] [page 124: Figure 3.4] [page 125: Figure 3.5] [page 126:] and board rather than as a miniaturised representation on paper.20
In the pre-paper world of the shipyard, design was thus not the same as construction, for frames were specified in advance by constructive geometry. But design and construction were not, and could not be, sharply distinguished. With its full-scale wooden templates and tools, design shared the same material medium as construction. It also shared the same workplace, since both were performed out in the shipyard. Moreover, all the evidence suggests that apprentices learnt the craft by observing and copying these operations in the workplace. Instruction was delivered informally, as directions and advice to be followed on the job.21 Oral and material culture were seamlessly joined.
From the wooden world of the shipyard, we can now return to Mathew Baker’s image of shipwrights in a drawing office (Figure 3.1; above, p. 109). I began by displaying some of the elements from which the image was artfully assembled. But now the wooden work of the shipyards demonstrates the extent to which the very practice of design on paper itself had to be constructed. Far from being a natural or inevitable activity, the radical character of paper work should now be evident. Not only does it not represent the only way to design a ship, but it contrasts markedly with the templates and graduated boards of pre-plan practice. With Baker, we are now [page 127:] removed from the busy world of the wooden shipyard: design is portrayed as inhabiting a space quite different from the work of actual construction. Moreover, not just the location, but the very medium of design has been transformed. The master works with dividers on the plan and section of a ship, translating the complex geometry of narrowing into miniaturised form through the technique of scaled drawing. Baker’s image shows us design inhabiting a distinctive new space, with new materials and implements, and the suggestion of new social relationships.
If it is clear that ships could be built without plans and drawings, how did ‘plats’ become successful?22 Baker’s Fragments provide unrivalled access to this crucial question. Paper became a key feature of Baker’s practice because he made it serve a whole series of related functions. Baker’s manuscript pages became a site on which technique, control, teaching, administration and the navy could be juxtaposed and combined. Fragments shows how Baker not only served his own interests through the use of graphic design and paper work, but enrolled the interests of others. By examining the didactic possibilities of Fragments and the integration of paper practice into the hierarchy of navy administration, I will indicate how ‘plats’ could help to redefine relationships and recruit allies. But first I investigate the more personal and private benefits which Baker derived from design on paper.
Paper could provide a medium of record and reference. Baker vigorously exploited this capacity. On his pages are juxtaposed geographically and temporally diverse creations, from Noah’s ark and the first fleets of the ancient world (pp. 1-3), [page 128:] to contemporary ships whose details he knew at first hand. Close to home, Baker included evidence of his own father’s ships.23 But he also ranged much more widely. Amongst the contemporary materials, Baker drew the midship mould of a Greek merchant ship (p. 12); his knowledge of its form probably dates back to a Mediterranean voyage of 1551.24
Baker also documented Venetian midship mould procedures, providing unique evidence of historical changes in their techniques (p. 11). The likely source for Baker’s awareness of Venetian practice is pointedly suggested by the navy quarterly accounts, where Baker’s name appears directly above that of a certain Augustino Levello.25 Levello was a Venetian shipwright who had originally been brought over to build galleys for Henry VIII but who then remained in English service for over 40 years.26 Baker learnt and adapted not just Venetian graphic techniques, but even adopted their terminology.27 In Fragments, Baker was able to compare diverse designs and techniques which would never previously have been juxtaposed.
Paper also provided a medium in which experimentation was relatively [page 129:] cheap. As well as recording the midship moulds of others’ ships, Fragments also shows Baker at work on new possibilities of his own. The rationale for his focus on these midship main frames is very explicit: ‘forasmuch as the goodness of every ship doth consist in the perfectness of the midship mould it is requisite [that] the same be perfectly made’ (p. 34). Typically, Baker’s midship moulds were drawn over proportional grids and made up of touching arcs of circles. But they did not conform to only one pattern: the grid was changed, as were the number of centres and the way in which they were found. Baker used the pages of Fragments as a medium in which to test new measures and ratios, varying parameters in order to assess their influence on the form of the hull. His most systematic exploitation of the possibilities opened up by design on paper appears in two numbered sequences of midship moulds. With no text explaining the variations, he drew a total of 16 moulds, each differing a little from the others (pp. 36-9, 42-3, 46-7).
Even when he came closest to prescribing a canonical form for midship moulds his trials did not stop; despite giving explicit and seemingly definitive instructions for the draught of a midship mould on one page, the accompanying drawing actually departed slightly from them. When drawing the upper futtock (topmost section of the mould) he carefully scribed the lines laid down in his text, but he did not ink them in. Instead, he scribed an alternative orientation and then finally settled for a third choice (pp. 34-5; see Figure 3.6).
Baker was seeking to achieve a new level of control over more than just the form of the midship mould. Whereas the most sophisticated template techniques worked with only the central section of the hull, Baker aspired to more: his rising and narrowing lines cover the whole length of the ship (p. 21, see Figure 3.7). Baker was [page 130: Figure 3.6] [page 131: Figure 3.7] [page 132:] attempting the complete specification of the form of the hull on paper.
But Fragments did not have an audience of only one. It was not a purely personal document. Despite the master shipwrights’ reputation for guarding the secrets of their craft, there are indications that Fragments was written for others too, and that the design practices that it reveals were embedded in wider relationships.28
One segment of the additional audience for Baker’s texts and draughts was the group of his pupils and apprentices. Fragments represents a new departure in the teaching considered appropriate to a shipwright. The didactic dimension of Fragments is suggested by Baker’s language: ‘in this division observe all the rules before taught’ (p. 40); ‘Now that I have showed how to know the tonnage of a ship ...’ (p. 154). Moreover, we know that he had apprentices. Even in his eighties, when he prepared his will, Baker still had two ‘servants’ to whom he bequeathed various ‘books and instruments of the art of shipping and moulds belonging to the same.’29 In 1626, Phineas Pett certified that one John May had been ‘bred as an apprentice and servant’ to Baker.30
The same Phineas Pett, himself a master shipwright to James I and Charles I, provides vital evidence of the character of Baker’s teaching. Despite much enmity between the two men in subsequent years, Pett was to recall in his autobiography that in the winter of 1595/6,
in the evenings, commonly I spent my time to good purposes, as [page 133:] in cyphering, drawing and practising to attain the knowledge of my profession, and I then found Mr Baker sometime forward to give me instructions, from whose help I must acknowledge I received my greatest lights.31
Pett’s testimony is of exceptional interest. Firstly, it specifies the area in which he supposed knowledge of his profession to lie: ‘cyphering, drawing and practising’. Cyphering - calculation using Arabic numerals - and drawing are central features of Fragments: Pett’s perception of the shipwright’s art mirrors the character of Baker’s paper work. In addition, primary responsibility for fostering this perception is ascribed to Baker, who was evidently encouraging and open with his knowledge, even though Pett was never his apprentice; in an (admittedly flattering) letter to Baker of 1603, Pett remarked that ‘although I served no years in your service, yet I must ever acknowledge whatever I have of any art (if I have any) it came only from you’.32
Pett’s casual comment that Baker’s instruction was given in the evenings also suggests a deeper point. Shipwrights traditionally learnt their trade by the observation and imitation of a master out in the shipyard. The art was passed on during the hours of the working day and the process did not demand literacy or formal numeracy. But Baker was sponsoring an alternative approach to teaching, carried out when work was over. Facility in calculation and draughting techniques was developed and literacy probably assumed. Baker was promoting a form of training separate from the exercise of the craft at the workplace. So not only design, but craft teaching too, was removed from the wooden world of the shipyard and transferred to a new space like that of [page 134:] Baker’s drawing office (Figure 3.1).33
The implications of this shift in the place of design and teaching are best exemplified not by the evidence of a shipwright but by Sir Robert Dudley (1574-1649), the illegitimate son of the Earl of Leicester. Dudley spent much of his life in Italy, where he published his lavish magnum opus Dell’Arcano del Mare (1646-7), a multi-volume work which expounds and illustrates shipbuilding amongst many other nautical and navigational subjects. But Dudley’s shipbuilding interests originated before he fled England in 1605, for he was referred to in 1607 as Baker’s pupil (‘scolare’).34 That Dudley should have had a shipwright as a ‘master’ is remarkable for, though illegitimate, he had been brought up in the ranks of the nobility. The relationship between master and pupil was surely only conceivable because Baker had rendered both teaching and design as paper practices, separated from the shipyard where common workmen exercised their trade.
Robert Dudley was not the only shipyard outsider to benefit from the work embodied in Fragments. In addition to its didactic context, Baker’s work also had an administrative significance, for design on paper was integrated into the navy’s decision-making process. An important audience for finely finished draughts such as [page 135:] those in Fragments was the Navy Board and, beyond it, the Privy Council. Indeed, shipwrights’ plats on occasion went to the highest authority in the land. In a letter of 1588, addressed to the three royal masters (Peter Pett, Richard Chapman and Baker), the principal officers of the navy requested that
the Plats of the Ships, Galleasses and Crompsters that were lately determined to be built should be set out fair in Plats and brought to my Lord Admiral that her Majesty may see them.35
Navy expenditure was a major drain on the national coffers. Yet those ultimately responsible for the military security and solvency of the realm were unlikely to have either experience or understanding of the dockyards and their products. Baker later recalled how Lord Treasurer Burghley had opened his house to the meetings of master shipwrights and Lords of the Council at which plats were displayed and resolved upon.36 By bringing proposed ships into the administrative chambers of state, plats made complex issues of performance and price directly visible to the Lords of the Council as well as the Navy Officers. As a tangible focus for the hard bargaining and negotiation which preceded the approval of new naval construction, the miniature representations of scaled drawings extended the financial and technical control available to both the naval and civil authorities.
At the same time as he used plans to serve the interests of his superiors, Baker was also promoting his own interests as an indispensable servant of the crown. Nor was this a game of merely nominal status; the stakes were high. Especially during the 1570s and 1580s there was almost continuous administrative upheaval and in-fighting, with a corresponding uncertainty over the exact distribution of naval [page 136:] responsibility and power. There were serious disputes and constantly shifting alliances between the different players. Insecurity and distrust were rife: ‘before, the master shipwrights did direct, but now they are to be directed; and being but hirelings were glad to please their master’.37 Paper design helped to bolster the role of the master shipwrights in this unstable environment, and to fend off threats to their position and prestige.
Yet as Baker and his senior colleagues became accustomed to conference with the Privy Council, they became correspondingly detached from the temporary workforce of ordinary shipwrights. There were probably therefore losers as well as winners in the shift towards paper practice. Large dockyards such as the Venetian Arsenal already possessed a hierarchy of expertise and authority, but Baker’s new skills consolidated the existing division of labour and elevated the master further above the ranks of his humbler colleagues.38 The master was now a more remote figure who could direct work from a distance; Baker is, for example, reported to have ‘moulded’ a ship, which was then framed by a close colleague.39 [page 137:]
Baker inserted his paper design work within the vertical hierarchy of apprentices, masters and governing authorities who practised and regulated naval shipbuilding. In doing so he was shaping a new place for design: a new physical location, a new position within the technical practices of the craft, a new set of materials, and a new social and administrative setting. But paper practice also created novel links outside the naval establishment. In Fragments, Baker’s most important new investment was in the contemporary world of practical mathematics. I therefore now turn to his horizontal integration of ship design with the mathematical arts.
3. MATHEMATICAL CONSTRUCTIONS
We have seen that Mathew Baker’s Fragments was a multi-purpose document. It was used as a repository for constructed ships, experimental designs and international comparisons; it consolidated technical control in the hands of the master shipwright; it embodied new materials for the teaching of the craft; and it included finely finished draughts suitable both for presentation and as a formal record of contractual accountability.
However, Fragments also had another use, as a site for calculation. Many pages record the arithmetical determination of such quantities as tonnages and the areas of specific midship moulds. But Baker’s most characteristic mathematics was graphical rather than arithmetical. There is a 20 page section of the manuscript which is especially striking, for it uses thick pasteboard rather than ordinary paper as a medium for proportional scales and graphical devices (p. 57ff.). Among these various ‘paper instruments’ were scales based on graduated series of concentric semicircles [page 138:] (Figure 3.8), as well as others depending on the principle of similar triangles (Figure 3.9). Both types embodied rules of proportions for dimensions such as moulded breadths or the lengths of masts and yards; a number still have index threads attached, while some show signs of extensive usage. Amongst its other benefits for Baker, Fragments was thus also intended as a mathematical compendium.
But Baker’s paper scales and instruments were more than just working tools. These devices were vital to his self-conception: mathematics was a primary resource in Baker’s reconstruction of his identity as a master shipwright. For, rather than the skill of manual craftsmanship with wood, Baker adopted a rhetoric of arithmetic and geometry. He rejected the work of older masters and charged that they had proceeded by mere rule of thumb. Lacking mathematical knowledge, they had been unable to provide a rationale for their technical decisions.
Before plots and demonstration were used the master workmen in those days had certain rules of proportion, but not such as agreed with art, for that they wanted the use of Arithmetic and Geometry for the searching out of those things that otherwise is impossible to be found (p. 28).
Even contemporaries who did use plans were open to criticism.
Although at this day there be many that use plots yet the best understandeth not the true making thereof, neither the truth of any circular line therein contained (p. 16).
For Baker, arithmetic and geometry were the ‘two supporting sciences’ (p. 33). Mathematics acted as the primary point of reference in bolstering his self-conscious disdain for traditional methods. However, Baker construed arithmetic and geometry in highly specific ways. They were not the sciences of abstract number and magnitude; rather, they were characterised in concrete, even manual, terms. [page 139: Figure 3.8] [page 140: Figure 3.9] [page 141:]
Arithmetic and its calculations were pre-eminently to be done ‘with the pen’. Baker’s pen-reckoning implicitly rejected the arithmetic of many contemporaries. Calculating ‘with the pen’ (or cyphering) meant using Arabic numerals. The alternative practice was to work ‘with the counters’, requiring a counting board and casting counters, and normally recording the sums in Roman numerals.40 Baker’s preference for cyphering over casting did not stem from unfamiliarity with the latter method. The shipyard clerks with whom he was in regular contact evidently reckoned with board and counters: the Navy accounts use Roman numerals to detail many payments to stationers for ‘casting compters’.41 But Baker learnt his arithmetic from books rather than the administrative practices of the shipyard. When he extracted roots and worked with the symbols of algebra he was drawing on texts such as Robert Recorde’s Whetstone of Witte (1557), which went well beyond the elementary calculations required for accounting.42
If the arithmetic of Fragments was done ‘with the pen’, the archetypical operation of geometry was the use of dividers and straight edge to produce midship moulds, plans and elevations. For Baker, each of these drawings was a ‘geometrical demonstration’ (pp. 34, 73). However, such ‘demonstrations’ were a ‘showing forth’; the term carried no connotation of proof. Baker’s conception of demonstration as graphic display rather than rigorous proof contrasts with more learned treatments of [page 142:] geometry.43 Yet his drawings were not casual sketches. Part of the apparatus of the ‘geometrical demonstration’ was the linear scale, which related the miniature ship on paper to the intended full size in wood. Working by the scale rendered Baker’s plats as exact depictions.44
Despite his graphical emphasis, Baker was not unaware of the Euclidean tradition. Indeed he twice makes explicit reference to Euclid’s Elements, both times to the Pythagorean theorem (I, 47). He first uses ‘the 47 proposition’ to find the hypotenuse of a right-angled triangle in the grid of a midship mould (p. 34). On the second occasion he cites not the theorem itself but a corollary added by the French mathematician and poet Jacques Peletier: ‘the first 47 proposition added by pelitarus’.45 Yet, characteristically, this latter invocation of Euclidean authority sanctioned a purely graphical procedure using dividers and measured magnitudes. Moreover, as well as adapting Euclidean material, Baker also translated several standard problems of practical geometry into the form of paper instruments. Textbook chestnuts such as the relations between squares and circles or cubes and spheres were converted into graphical format (pp. 66-7), while Baker also discussed the volumes of cylinders and prisms (p. 32).
For Baker, arithmetic and geometry were characterised by the operations of pen, dividers, scale and straight edge. Arithmetic and geometry complemented each [page 143:] other but were independent; together they served as the ‘two supporting pillars of every art’ (p. 34). Hence, in resolving a question one could work with or without number (p. 40). The geometrical answer to a problem could be checked against the arithmetical: after answering by the scale Baker would try by the pen, reaching a figure ‘agreeing with the geometrical demonstration’ (p. 73).
The pen and the demonstration had their respective advantages and disadvantages. Proportional scales embodying the principle of similar triangles (such as that in Figure 3.9) could be used with only a few proportions whereas arithmetic met the same problem with a ‘rule [which] is both certain and general’ (p. 65). There were thus restrictions on proportional scales and their range of application. But they were often more appropriate to Baker’s design practice than the pen:
although this scale doth not give so precise the fraction as the pen doth, yet it doth give the true proportion of the lines which in the drawing of plats is better than to have it given in number (p. 68).
Moreover, the achievement of precision in cyphering could require calculations which Baker was happy to avoid. The rules he devised for tonnage frequently called for the extraction of cube roots. Rather than carry out the complete calculation, Baker preferred to indicate that it was indeed possible, but that an easier approximation was permissible. At the end of a series of calculations peppered with arithmetical errors, he remarked that
although these [roots] are not extracted so near as they might be yet is it within one tenth. My desire is rather to show the rule & reason to do the same than the preciseness thereof ... To those that hath been brought up in the trade of a Carpenter & that hath the knowledge of extracting of roots this may suffice (p. 153).
There cannot have been many shipwrights ‘brought up in the trade of a carpenter’ who were able to extract square and cubic roots. Through the rhetoric of arithmetic and [page 144:] geometry as well as the adoption of specific mathematical techniques, Baker was prescribing a new identity for the shipwright. Combining experience of the craft with imported mathematical knowledge and values, the shipwright was now to be identified as a mathematical mechanician.
Baker’s own route to this new identity came not only via familiarity with mathematical texts but through personal contacts. The material in Fragments suggests successful collaboration within the naval and mathematical community, as well as at least one instance of creative discord. Examining these instances highlights Baker’s personal as well as intellectual integration with the small group of contemporary mathematical practitioners.
Baker’s measuring scales provide a first, indirect, hint of his affiliations. Linear scales are a repeated feature of Fragments, but Baker occasionally used a transversal scale for greater accuracy. These square scales, with diagonal lines running across horizontals, were graduated into divisions corresponding to one inch (Figure 3.10). Just as ordinary linear scales had been only recently introduced into English map and chart making, so transversals were considered a novelty in astronomical instrumentation. Thomas Digges recommended their use in 1573 for his astronomical cross staff, attributing this improved method of graduation to the navigator and instrument maker Richard Chancellor (d. 1556), ‘peritissimus & ingeniosissimus Artifex Mathematicus’.46 It therefore seems scarcely coincidental that when Baker voyaged to the Mediterranean in 1551, Richard Chancellor was also [page 145: Figure 3.10] [page 146:] among the crew.47
On the same page as one of Baker’s diagonal scales is a condensed ship draught which gives further clues to his mathematical associates. This abbreviated plat shows the stem, stern and midship mould of a small ship labelled the ‘Judeth - Borowgh’ (p. 6, see Figure 3.10). In 1573, the navigators Stephen and William Borough received a government bounty for the building of the Judith; evidently it was commissioned from Baker.48 William Borough later became a permanent officer of the navy and was an ally of Baker both in the internal politics of navy administration as well as during other projects such as Dover harbour.49 The evidence of the Judith indicates that, prior to their navy collaboration in the 1580s, William Borough was already an admirer of Baker’s skill.
One small remnant of contact between Borough and Baker is their use of the same form of decorated linear scale, by Baker in his ship draughts, by Borough in his sea charts.50 But they shared more substantial interests. Aside from his concerns with mathematical navigation and magnetism, Borough also dealt with questions of shipbuilding. In particular, he compiled a memorandum which not only laid down proportions for various types of merchant and naval ship but also offered a method for [page 147:] tackling the thorny question of tonnage determination.51 Less surprisingly, Baker also treated the qualities required in different classes of ship (eg p. 40). Moreover, Fragments records his efforts to grapple with tonnage in a way which matches the arithmetical techniques propounded by Borough (pp. 65, 153-4).
Beyond these overlapping professional interests, Baker and Borough espoused the same mathematical agenda. Baker’s emphasis on the primary role of arithmetic and geometry is also found in Borough’s Discours of the Variation of the Cumpas (1581). In the preface to that text Borough portrayed arithmetic and geometry as ‘the grounds of all Science and certain arts’, and he paused to commend those mechanical practitioners who
by the studious practice and exercise in these arts have attained to rare and singular knowledge: In Architecture, Vitruvius the Roman: In painting that famous German Albertus Durerus: And in building of Ships, Mathew Baker our countryman.52
To be bracketed in such elevated company was high praise indeed. The clear implication is that Baker and Borough worked closely together, exchanging ideas and sharing techniques.
Baker was in contact with Chancellor (d. 1556) during his early career. Borough (d. 1598) was a principal ally of Baker’s maturity. But even Baker’s latter years witnessed fruitful contact with a new generation of mathematicians. Most remarkable is the evidence of his connection with Thomas Harriot, probably the most expert English practitioner of the mathematical sciences in the early 17th century. [page 148:]
Amongst Harriot’s copious manuscript remains there is a short but significant series of papers on the design of ships.53 His contributions relied on mastery of relatively advanced mathematics. He raided the repertoire of conic sections for ellipses to represent the arcs of frames and employed cubic and quartic curves to capture the subtle risings and narrowings of a ship’s lines. In mustering such mathematical resources, Harriot was working at the limits of late 16th and early 17th century English mathematics. Yet he was not working in isolation. Alongside his exposition of a new hyperbolic technique to generate mast dimensions for ships built in proportion, Harriot jotted down a note for his own reference: ‘Invented this February 28 1608 and gave it to E Marlow for Mr Baker the shipwright’.
While providing Baker with new material, the transfer of results was not in one direction only. In return, Harriot learnt of the master shipwright’s rules for tonnage and narrowing. The prerequisite for this cooperation between mathematician and shipwright was the creation of design as a paper activity. Only after ships were available for study as miniaturised portable representations could the armoury of advanced mathematics be brought to bear on the work of the shipwright. Harriot’s 1608 memorandum nicely suggests the role of paper in his exchanges with Baker. While Harriot and Baker had presumably met, personal contact was not essential to their continued relationship: communication was possible at a distance and it was expected that new results could successfully be sent on through an intermediary.
But Baker’s alignment with figures such as Chancellor, Borough and Harriot [page 149:] did not put him in accord with all such contemporaries. Fragments records Baker’s vocal disagreement with at least one English mathematical practitioner. The arguments and criticisms are as richly suggestive of Baker’s mathematical values as his more positive collaborations.
On the first of his pasteboard pages of proportional scales, Baker composed a poem of doggerel verse (p. 57). The final lines targeted a certain ‘patching bourne’, who ‘hath patched together the works of other men, and now to sale he paints it out with his unlearned pen’. The ‘bourne’ in question was the author William Bourne (c.1535-1582) who, among his various mathematical and practical texts of the 1570s and 80s, had published some material on shipbuilding in his Treasure for Travellers (1578).54
Baker’s implied accusation of plagiarism may have been aggravated by personal friction. There was certainly ample opportunity for contact: in 1574 Bourne appeared on the navy payroll when he was installed as master gunner at Upnor, a castle built to protect the fleet at anchor in Gillingham Water.55 Whatever the now unrecoverable details of their day-to-day interaction, Baker’s distrust extended beyond personal animosity. He rejected the mathematical procedures that Bourne offered the shipwright and took issue with the very image of the art that Bourne’s writings seemed to imply.
In the Treasure for Travellers, Bourne sought to show how ships could be [page 150:] built in proportion.56 The aim of this process, which was rapidly becoming a standard contemporary topic, was to replicate the qualities of a successful ship.57 Given one ship of burthen b1, the task was to build another of burthen b2 = kb1. In summary form, Bourne’s rule for each dimension d2 of the second ship was
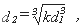
where d2 corresponds to dimension d1 of the first ship. Hence, if a ship of 100 tons has a breadth of 20ft, a ship of 125 tons built in proportion should have a breadth of
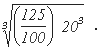
But Bourne knew that ‘the most part of men cannot extract the cubic root, for that kind of Arithmetic is very hard, and not easy to be learned’.58 So he gave a series of approximations for standard proportions. For example, in building a second ship one quarter larger than a first, every relevant dimension of the first should be measured, divided into 4 equal parts and the corresponding dimension of the second ship found as 4⅓ parts. Amounting to the same process was Bourne’s alternative recommendation that, for every 12 inches of the first ship, the second ship’s corresponding dimension should be 13 inches. Similar, ‘reasonable exact enough’ [page 151:] approximations were given for ships up to 8 times larger than a given ship.59
Baker offered a graphical counterblast to Bourne’s arithmetical working with the pen. Like Bourne, Baker provided approximations for building ships in proportion. But he did so through the medium of proportional scales. On one of his pasteboard pages, Baker drew up a scale to ‘show the proportion that one ship doth bear to another’ (p. 65; see Figure 3.11). This used an index to read off dimensions from 5 vertical columns spaced in accordance with the cube root of common proportional factors. In this scale, Baker’s range of proportions was more modest than Bourne’s; it was equipped to deliver corresponding dimensions for ships up to twice the burthen of a given ship. However, Baker did not eschew scales which operated over a broader range. On another pasteboard page he drew a scale of the same type but which was intended to cover ships differing in proportion by a factor of 10: ‘These are cubic scales of proportions serving from 10 tons to a 100 & from a 100 to a 1000.’ Baker’s enthusiasm is evident from a later note, added in a different ink: ‘marvellous is the use of this scale & serving to great purpose. Infinite are the questions that may be answered by this scale’ (p. 77).
Similar advantages could be obtained from semicircular scales; commenting on one intended for the proportions of ropes and squares, Baker noted that
this scale is not like the brabble that Bourne makes about in the proportion of ropes, the which is tedious and yet not general and serveth but to a few numbers by him limited (p. 76).
As well as replacing Bourne’s arithmetical approximations by various proportional scales, Baker quite explicitly tackled Bourne’s more exact and general method of finding dimensions in proportion. Bourne required that the shipwright raise every [page 152: Figure 3.11] [page 153:] relevant dimension to the third power, multiply each cube by the proportional factor and then extract the cube root of the product. Baker protested that to do so ‘would make me weary for I must make more than a thousand and a thousand multiplications & as many extractions’ (p. 26). Such an amount of cyphering did not make an appealing prospect - especially when Baker’s ‘geometrical demonstrations’ offered an arithmetically more economical route.
Baker’s scaled plats of ships in plan, section and elevation portrayed the major elements of the hull. Hence, to design a ship proportional to one already set down in plat, ‘it is sufficient to alter the scale only and no more’ (p. 21). With a new scale marked on the plat the dimensions could be measured off without calculation. The rescaling itself involved only one multiplication and one extraction and so ‘to him that hath the extracting of roots the matter is very easy & to be done with the pen’ (p. 26).
Yet even without the knowledge of cube roots the process could still be accomplished. For the benefit of the ‘mechanical workman’ lacking arithmetic, Baker applied ‘a certain rule that I found demonstrated in Albartus Dureri in his book of Geometry’ (p. 26). Baker had made use of Dürer when constructing his image of shipwrights at work in a drawing office and he had been placed on an equal par with Dürer by William Borough. But here, Baker was going beyond the realm of visual and textual rhetoric to borrow in detail from Dürer’s geometric techniques.
Baker’s source was Dürer’s Underweysung der Messung (1525), one of whose topics was the classical problem of how, given one cube, to construct another of twice the volume. Dürer presented a generalised solution to the problem of [page 154:] doubling the cube, providing a means of constructing cubes in any desired proportion. In other words, given the side of one cube, Dürer found the side of another cube either twice as large or whose volume was in any other proportion. Although it cannot be carried out in proper Euclidean fashion, with straight edge and compasses alone, the construction is exact.60
Baker adapted Dürer’s method to his own end of rescaling the draught of a ship. Rather than using the sides of cubes, he worked with ship dimensions. Starting with, for instance, a line representing the depth of an already drawn ship, Baker arrived at a second line representing the depth of the corresponding proportional ship. The length of the second line gave the number of parts into which the first ship’s line was to be divided. After redivision, the first line served as a scale from which any depicted dimension of the second ship could be read off (see Figure 3.12).
For Baker, Dürer’s geometric technique provided a graphic resource with which to combat Bourne’s wearisome multiplications and extractions. But it also exposed the larger inadequacies of Bourne’s treatment of shipbuilding. Bourne was charged with setting forth his Treasure for Travellers
to the discredit of workmen how having a little understanding in the extracting of a root would make the world believe that all the knowledge of ship making did consist only in the same (p. 26).
Baker was able to show that not only did the art of the shipwright consist of more than [page 155: Figure 3.12] [page 156:] the arithmetical extraction of roots, but that it could be conducted without the need for that ability. Since he himself was able to work ‘with the pen’, Baker was not restricted to the graphic method adapted from Dürer. His principal point in adducing Dürer was thus to circumvent and rebut the illegitimate claims he discerned in Bourne’s pronouncements.
Yet the disagreement with Bourne serves to underline rather than undermine Baker’s engagement with contemporary mathematical practice, for both were tackling the same questions of building ships in proportion. Disagreement sprang not from their command of arithmetic but from Baker’s conception of geometry as the necessary complement of arithmetical work. Both arithmetic and geometry were essential as the ‘two supporting sciences’ of Baker’s paper work of plats and scales.
Mathematics was thus a crucial point of reference in Baker’s reconstruction of ship design and the role of the master shipwright. As a rhetorical resource, he used it to differentiate himself from earlier shipwrights; geometry was identified with the preparation of draughts, while arithmetic was used to calculate lengths, areas and capacities. Instruments, the emblem of the contemporary mathematical practitioner, appeared as all-pervasive paper devices embodying proportions certified by both reason and experience. Moreover, in placing his design work under the banner of mathematics, Baker drew on the expertise of mathematical practitioners to gather persuasive power and practical assistance from beyond the traditional confines of the shipwright’s craft.
A final illustration of the extent to which the culture of mathematics was crucial to Baker’s self-understanding is provided by his only major foray into the [page 157:] traditional full-scale work of the shipwright. Baker had developed a new way of prescribing and varying the curves of narrowing and rising, not on paper but out in the shipyard, by means of ropes and boards. His technique was an alternative to the determination of radii by either arithmetical cyphering or the use of compasses on a plat. It was announced as
a mechanical demonstration devised or first invented by Mathew Baker for the carpenter unlearned in arithmetic & geometry, by which is found all circular divisions needful to the making of ship, galleon, galley or whatsoever (p.33; see Figure 3.13).
Baker’s flexible and general-purpose device was similar to some of the mechanically generated and varied curves proposed by Dürer.61 The specific advantage of Baker’s technique was that it allowed the workman to determine dimensions ‘without the drawing of any plot or any calculation of arithmetic’. Baker cast himself here in the role of the mathematician ministering to the needs of the merely ‘mechanical workman’. In shaping this mathematical role for himself, he drew on the tradition of classical geometry to elevate his own achievements. When recording the invention of his new ‘mechanical demonstration’, Baker quarried the anecdotal lore of the Euclidean corpus as a source of materials for his own self-interpretation:
If Pythagoras did so much joy for the finding out of the doubling of a square by the line diagonal that he offered to his unknown gods an ox in sacrifice, I say I have good cause to give our living and known god thanks for this invention so necessary for my unlearned countrymen in the two supporting sciences (p. 33).
Baker could have found the familiar story of Pythagoras’ celebration not only in classical sources such as Vitruvius but as part of the editorial embroidering of recent [page 158: Figure 3.13] [page 159:] editions of Euclid.62 With Pythagoras as a role model, Baker was differentiating himself from his ordinary colleagues. Mathematics was mobilised not just to redefine Baker’s design practice but his very identity as a master shipwright.
4. MATHEMATICAL PRACTICE AND NAVAL ARCHITECTURE
Mathew Baker’s paper design was directed towards the advance specification of the ship’s hull and his mathematical reconstruction of shipbuilding embedded new priorities and values within the practice of the art. In this transformation, the geometrical determination of shapes and the arithmetical calculation of dimensions emerged as principal tasks of the master shipwright. Yet, if we inspect a surviving ship of the period, such as the English Mary Rose or the Swedish Vasa, the frames of the vessel are almost invisible.63 From the outside, we see the skin of external planking, while inside there is additional planking as well as the strengthening structures of keelson, riders, knee timbers and internal wales. Ships were much more than just carefully defined shapes; they had to be strong enough to serve as sailing platforms for men, stores and increasingly heavy guns. Fragments contains almost nothing on the ship as a structural and functional artefact. Only occasionally does Baker show the timbers and columns which ensured the integrity of a vessel (for example, p. 19). [page 160:]
Fragments is thus a partial document. It represents not a systematic presentation of the craft of shipbuilding in wood but an exploration of the possibilities opened up by mathematics and design on paper. Through geometry and arithmetic, questions of shapes and proportions were separated out from the rest of the art. The very particular direction of development which Fragments embodies is strikingly evident by contrast with sources from other traditions.
One of the most articulate contemporary presentations of shipbuilding was that offered by the Portuguese author João Baptista Lavanha in his incomplete Livro Primeiro da Architectura Naval.64 During a career spanning many disciplines, Lavanha taught cosmography, geography, topography and mathematics, and was an author of nautical treatises and chronicles. He also held important state offices; he was, for example, appointed Engineer to the King of Portugal in 1587. Contact with contemporary shipbuilding was thus just one aspect of a larger cycle of learned, didactic and technical activities.
Lavanha’s identification of shipbuilding as naval architecture provided a classically sanctioned model for the treatment of the craft. The opening chapters of his Livro Primeiro draw directly on book I of Vitruvius’s De Architectura for a definition of architecture and its six parts or principles. But though he quoted, paraphrased and elaborated on Vitruvius, Lavanha was not a slavish imitator. His stress on design and the mathematical arts in the formation of the (naval) architect, and on the importance of models as a check on building proposals, is closer to the [page 161:] recommendations of Alberti than Vitruvius.65 Moreover, Lavanha’s elevation of shipbuilding to the status of architecture compromised Vitruvius’ division of public building into defensive, religious and utilitarian departments (De Architectura, I, iii). Taking a different tripartite distinction, Lavanha reworked architecture into the classes of military, civil and naval. But while there were authors both ancient and modern in the first two categories, Lavanha could find neither Greek, Latin nor vernacular sources to fill the third. He was simultaneously creating the space and the justification for his own work.66
By integrating shipbuilding with architecture, Lavanha committed himself to following the well-established practices and precedents of the parent art. As with Vitruvius and Alberti on architecture, Lavanha devoted sustained attention to the materials of shipbuilding. He discussed the different varieties of timber and their respective qualities and uses; he considered the appropriate seasons for cutting and preserving timber; he reviewed the other materials such as iron, linen, tar, pitch and lead; and he even offered a brief disquisition on the destructive effects of the notorious teredo ship-worm.67
In England, by contrast, connections between architecture and shipbuilding [page 162:] were noted in passing, but not intensively developed. Under the title of ‘naupegie’, John Dee found a place for shipbuilding in his Mathematicall Praeface to the first English Euclid (1570). Dee subsumed naupegie (along with housing and fortification) as one of the three branches of architecture, just as Lavanha was later to do.68 Thomas Digges later made the same identification with his unredeemed promise to publish a ‘brief Treatise of Architecture Nautical’.69
Though Dee’s discussion of architecture gave prominence to Vitruvius and particularly Alberti, there is no evidence that his references had any affect on Fragments. Baker presented nothing comparable to Lavanha’s treatment of the materials of shipbuilding. Indeed, aside from a short complaint about the quality of wood brought to the shipyards by navy purveyors (p. 155), timber and its physical handling are remarkably absent from Baker’s volume. The other materials of the trade are not even mentioned. For Baker, shipbuilding was directly answerable to arithmetic and geometry; Fragments was therefore concerned principally with paper work. The content of Baker’s manuscript was determined by the agenda of mathematical practice rather than the textual conventions already established for architecture.
Baker’s Fragments set the pattern for an English tradition of shipbuilding texts which dealt primarily with the arithmetic and geometry of hull form. While we know little about how Baker’s work was used within the naval dockyards themselves, it is clear that shipbuilding became firmly established as one of the mathematical arts [page 163:] in England. One stage of that process is revealed by Fragments itself. Although mostly by Baker, there are sections in another hand. These additions, which range from dialling and mathematical instruments to magnetism and shipbuilding, were supplied by John Wells, to whom Baker bequeathed Fragments and other volumes.70 Wells was a navy storekeeper at Deptford, a mathematical practitioner who published on sundials, and an associate of such London mathematical professors as Henry Briggs and Henry Gellibrand.71
Amongst his other mathematical activities, Wells assisted Briggs in the construction of logarithmic tables in the years after Napier’s first publication in 1614.72 Wells’ perception of the mathematical character of ship design and its place in the scheme of mathematical arts is suggested by his assimilation of logarithms to shipping questions (e.g. p. 91). Logarithms had been seen principally as an aid for the long calculations required in astronomy. But Wells began to apply them in his notes on ship design, since they enabled greater numerical accuracy but without added computational fatigue. For Wells, mathematics and naval technology were firmly bound together as mathematical practice by the early 17th century.
Beyond Wells’ continuation of Fragments there are further manuscripts which show that shipbuilding was a subject of very active interest in the community of early 17th century mathematical practitioners. Thomas Harriot’s shipbuilding papers have already been noted and their level of sophistication was matched by several other [page 164:] surviving texts.73
Baker’s work thus embodied a programme which was pursued by his mathematical colleagues and successors. Materials and structures were given less prominence than the mathematics of hull design. Logarithms and higher order curves supplemented the resources which Baker had himself been able to muster, and these increasingly sophisticated mathematical techniques were presented in more systematic treatises. The development of the paper geometry and arithmetic of Fragments rapidly made English shipbuilding the most mathematically advanced of any country in Europe.
The creation of ship design as a mathematical art offered benefits both to Baker and also to the mathematical practitioners who tackled shipbuilding questions. Baker’s success in adopting explicitly mathematical techniques reflected back on the practitioners and supported their claims to utility and status. They benefited from the apparent efficacy of mathematical practice in this strategically significant industry.
But, as an elite mechanician, Baker also stood to gain. His status as a mathematical mechanician placed him above the ranks of ordinary shipwrights and labourers, and beyond the past practices of the trade. Baker’s reputation transcended the local realm of the shipyards and was transferred out into the wider world of print culture. William Borough had praised Baker in 1581 as a worthy peer of Vitruvius and Dürer, while the navigator John Davis pressed further accolades on Baker in his [page 165:] Seaman’s Secrets of 1595. Davis mentioned ‘the mechanical practices drawn from the Arts of Mathematick, [in which] our Country doth yield men of principal excellency’:
As M. Emery Molyneux for the exquisite making of Globes bodies, and M. Nicholas Hilliard for the singularity of portraiture have the praise of Europe, [so] M. Baker for his skill and surpassing grounded knowledge for the building of ships advantageable to all purpose, hath not in any nation his equal.74
Davis very likely knew Baker, and Borough certainly did. But once his name was in the public domain Baker became a point of reference for commentators who had probably never met him. Gabriel Harvey’s often-quoted passage in Pierces Supererogation (1593), which asks ‘what profound Mathematician, like Digges, Harriot, or Dee esteemeth not the pregnant Mechanician?’, bracketed Baker with such other ‘expert artisans’ as
Humphrey Cole, a Mathematical Mechanician, ..., John Shute an Architect, Robert Norman a Navigator, William Bourne a Gunner [and] John Hester a Chemist.75
What did this miscellaneous group have in common? John Hester’s presence punctures any attempt to link them through an adherence to the programme of the mathematical arts. Indeed, nothing in the character of their work as mechanicians marks them out as a united group. Rather, they were linked together by their appearance in print: all of these six mechanicians had either published books themselves or been referred to in the texts of others. Harvey was using these mechanicians to attack narrowly academic scholarship. Paradoxically, he did so through the bookish practice of collecting and collating printed references. Cut loose from the paper work of mathematical design by the approving references of friends, Baker’s fame was available for circulation in the public paper worlds of others.
FOOTNOTES
1. W.G. Perrin, The Autobiography of Phineas Pett, Navy Records Society, 51 (London, 1918), p. 178.
2. Pepys Library, Magdalene College, Cambridge, PL 2820, p. 8. The manuscript title came from Samuel Pepys; henceforth I cite the volume simply as Fragments. My in-text references to the volume are to page numbers. For a discussion of Fragments, R.A. Barker, ‘Fragments from the Pepysian Library’, Revista da Universidade de Coimbra, 32 (1986), 161-78.
3. On the general significance of paper as a medium, see Bruno Latour, ‘Visualization and cognition: thinking with eyes and hands’, Knowledge and Society: Studies in the Sociology of Culture Past and Present, 6 (1986), 1-40. Many of my subsequent specific comments on the uses of paper develop points in Latour’s suggestive account.
4. For Baker’s 1562 mastership: Bodleian Library, Rawlinson MS. (hereafter Bodl. Rawl.) A 200, f. 17r-v (cf. f. 10r where Baker is not described as master). For his appointment as a royal master in 1572: Calendar of Patent Rolls, Elizabeth, V (1569-72), p. 466 (no. 3303).
5. Perrin (footnote 1), pp. xx-xxi.
6. BL Add. MS. 7968, ff. 43r, 52r.
7. For the Pett family, see Perrin (footnote 1).
8. Bodl. Rawl. MS. A 203. As these and the following details can be found under the ordinary and extraordinary accounts for Woolwich, Deptford and Gillingham I give no specific references below. The same archive holds quarterly accounts for four other years: Bodl. Rawl. A 200 (1562 and 1563); A 201 (1570); and A 202 (1574).
9. A.P. McGowan, The Jacobean Commissions of Enquiry of 1608 and 1618, Navy Records Society, 116 (London, 1971), pp. 71 and 231 for Baker’s depositions to the 1608 Commission of Enquiry. Note too the evidence given by Edward Stevens (ibid. pp. 51 and 53). Baker went on a trip of this kind in 1562, taking two shipwrights to work on ‘the hewing and squaring of ix great Elms at Beddingtun for keels for her highness’s Ships’ (Bodl. Rawl. MS. A 200, f. 19r).
10. For a comparison with the Venetian example, P. Burke, Tradition and Innovation in Renaissance Italy (London, 1974), p. 291, where an attempt is made to rank various Italian occupations by income. Out of a total of 26 occupations, the Venetian master shipwright comes seventh equal.
11. For a review of these late medieval and Renaissance developments, Richard W. Unger, The Ship in the Medieval Economy 600-1600 (London, 1980).
12. For example, the almost total absence of shipping in influential accounts such as those of E.S. Ferguson is very striking: ‘The mind’s eye: nonverbal thought in technology’, Science, 197 (1977), 827-836; ‘La fondation des machines modernes: des dessins’, Culture et Technique, 14 (1985), 183-208; and Engineering and the Mind’s Eye (Cambridge, Mass., 1992).
13. Fausto to Giovanni Battista Ramusio in Epistolae Clarorum Virorum (Venice, 1556), f. 93v. On Fausto, F.C. Lane, Venetian Ships and Shipbuilders of the Renaissance (Baltimore, 1934), pp. 64-71 and P.L. Rose and S. Drake, ‘The pseudo-Aristotelian "Questions of Mechanics" in Renaissance Culture’, Studies in the Renaissance, 18 (1971), 65-104, pp. 77-8.
14. On these manuscripts, R.C. Anderson, ‘Italian naval architecture about 1445’, Mariner’s Mirror, 11 (1925), 135-63, idem, ‘Jal’s Mémoire no. 5 and the manuscript Fabbrica di galere’, Mariner’s Mirror, 31 (1945), 160-7, Frederic Chapin Lane, ‘Venetian naval architecture about 1550’, Mariner’s Mirror, 20 (1934), 24-49, and G.B Dosio (ed.), Ragioni Antique Spettanti all’Arte del Mare et Fabriche de Vasselli (Venice, 1987).
15. The fullest accounts appear in the works of Fernando Oliveira and João Baptista Lavanha. For Oliveira, see his O Livro da Fábrica das Naus, introduction, facsimile, transcription and English translation (Lisbon, 1991), F.C. Domingues, ‘Observation and knowledge in Portuguese ship construction of the 16th century: the treatises of Fernando Oliveira’ (unpublished translation by R.A. Barker of a paper given at the Fourth International Reunion for the History of Nautical Science and Hydrography, 1983), and three papers by Eric Rieth in Neptunia: ‘Les écrits de Fernando Oliveira: un témoinage sur la construction navale de la seconde moitié du XVIe siècle’, 165 (1987), 18-25; ‘Un système de conception des carènes de la seconde moitié du XVIe siècle’, 166 (1987), 16-31; ‘Remarques sur une série d’illustrations de l’Ars Nautica (1570) de Fernando Oliveira’, 169 (1988), 36-43. Lavanha’s work was first published in J. da G.P. Barata, ‘O "Livro Primeiro da Architectura Naval" de João Baptista Lavanha’, Ethnos, 4 (1965), 221-98; on Lavanha, see below, section 4. Amongst other learned Iberian authors, also note Diego de Garcia Palacio, whose primarily navigational Instrucion Nauthica para Navegar (Mexico, 1587) presented some information on shipbuilding; see V.D. Tate, ‘The Instrucion Nauthica of 1587’, American Neptune, 1 (1941), 191-5. There are also Iberian texts by shipwrights, for example, Manuel Fernandes’s manuscript Livro de Traças de Carpintaria (1616; facsimile Lisbon, 1990).
16. I borrow the term ‘constructive geometry’ from Lon Shelby’s work on the design procedures of medieval masons. See in particular ‘Mediaeval masons’ templates’, Journal of the Society of Architectural Historians, 30 (1971), 140-154, ‘The geometrical knowledge of mediaeval master masons’, Speculum, 47 (1972), 395-421, and Gothic Design Techniques. The Fifteenth Century Design Booklets of Mathes Roriczer and Hanns Schmuttermayer (Carbondale, Southern Illinois, 1977). For overviews of dockyard design techniques: R.A. Barker, ‘Many may peruse us: ribbands, moulds and models in the dockyards’, Revista da Universidade de Coimbra, 34 (1988) and Sergio Bellabarba, ‘The ancient methods of designing hulls’, Mariner’s Mirror, 79 (1993), 274-92.
17. Carvel was a relatively recent introduction in England. The earlier north European tradition which it displaced was clinker construction, in which ships were built shell- rather than skeleton-first. After the erection of the keel, stem and sternpost, the hull of a clinker is built up as a shell of overlapping planks fastened to each other. Strengthening transverse frames are added afterwards. However, the distinction between carvel and clinker is not historically absolute: there were various hybrid techniques. On carvel, clinker and hybrid construction, see O. Hasslöf, ‘Carvel construction technique: nature and origin’, Folk-Liv, 21/22 (1957/8), 49-60 and ‘Main principles in the technology of shipbuilding’, in Hasslöf et al. (eds), Ships and Shipyards, Sailors and Fishermen, trans. M. Knight and H. Young (Copenhagen, 1972), 27-72.
18. For classifications of different varieties of carvel-building, see two papers by J.P. Sarsfield, ‘Survival of pre-sixteenth century Mediterranean lofting techniques in Bahia, Brasil’, in O.L. Filgueiras (ed.), Local Boats, British Archaeological Reports International Series, 438, part 1 (Oxford, 1988) and ‘Master frame and ribbands: a Brazilian case study with an overview of this widespread traditional carvel design and building system’, in Carvel Construction Techniques, Oxbow Monograph, 12 (1991).
19. Oliveira (footnote 15), pp. 177-83 (facsimile, pp. 91-106). For Venetian sources, see Anderson, ‘Italian naval architecture’ (footnote 14), pp. 153-4 and F.C. Lane (footnote 14), pp. 29-31. The Italian use of the technique was not restricted to only Venetian shipwrights; Neapolitan usage is recorded in Bartolomeo Crescentio, Nautica Mediterranea (Rome, 1607), on which see the note in Mariner’s Mirror, 69 (1983), 305-6 and the corrections in 70 (1984), 87-8.
20. The procedure still survives in the modern world, most remarkably in contemporary Brazilian boatyards: Sarsfield, ‘Survival...’ (footnote 18). Kostas Damianidis has documented related techniques for 19th and 20th century Greece, see ‘The survival of moulding boatbuilding in an old boatyard in the Aegean’ (unpublished) and ‘The diachronic "road of dialogue" of Mediterranean shipbuilding: some methods for controlling the form of a vessel’, in Cultural and Commercial Exchanges between the Orient and the Greek World (Athens, 1991), 97-108. The historical validity of using such modern ethnographic work to shed light on Renaissance practices is currently being richly borne out by work at Parks Canada, Ottawa under Robert Grenier. Working with scale models of the surviving timbers of a wrecked 16th century Basque whaler, Brad Loewen is reconstructing the hull of the vessel using the techniques of adjustable templates.
21. Unger (footnote 11), pp. 241-2.
22. Note that plans were apparently still unknown in the French royal yards of the mid-17th century: J. Boudriot, ‘Evolution de la conception des vaisseaux royaux’ and E. Rieth, ‘Quelques remarques sur la conception des bâtiments de mer du moyen-age au début du XVIIIème siècle’, both in Résumés des Communications des 3èmes Journées D’Archéologie Navale; 6-8 décembre, 1985 (Musée de la Marine, Paris, 1985).
23. Fragments, p.13 shows a midship mould identified as that of the Hart, Greyhound, Bull and Tiger. A list of ships in the navy of Edward VI in Pepys Library, PL 1266, pp. 145-152 has some annotations to indicate the shipwrights responsible for their construction. The Hart, Bull and Tiger are all identified as by James Baker (pp. 147-8).
24. For the voyage, R. Hakluyt, The Principal Navigations, 12 vols (Glasgow, 1903-5), V, pp. 71-6. Baker identifies the Greek merchantman as a ‘screatse’. It may be related to or even identical with the Turkish ‘skryasas’ mentioned in the Hakluyt account, p. 73. Baker observed other procedures on this voyage; for example, he refers in Fragments to Sicilian and ‘Candian’ practices (p. 40). Presumably it was also at this time that he acquired the information or interest behind his map of the Peloponnese (p. 4).
25. For the juxtaposition of Baker and Levello: Bodl. Rawl. MS. A 201, ff. 65v, 68v, 71r-v and 74v.
26. T. Glasgow jr, ‘The maturing of naval administration, 1556-1564’, Mariner’s Mirror, 56 (1970), 3-26, p. 10. For Levello’s duties: Bodl. Rawl. MS. A 200, f. 9v.
27. Fragments, pp. 16, 23. Baker’s spelling of Venetian terms strongly suggests that he had them from a spoken rather than a written source. The two most striking instances are on p. 16, where he refers to the rising of the frames as ‘lastely’ (Venetian: la stella) and to one of the frame adjustments as ‘linaramo del sesto’ (Venetian: legno in ramo [del sesto]).
28. For a typical learned witness of craft secrecy, see G. Fournier, Hydrographie (Paris, 1643), p. 16: ‘among 400 or 500 ship carpenters one will scarcely find three or four who know the lines and proportions, because the masters are so protective (jaloux) of their knowledge and skill’.
29. PRO Prob 10/305, and also in PRO PCC 83 Capell (Prob 11/122, f. 140v).
30. PRO SP16/21/65.
31. Perrin (footnote 1), p. 7.
32. Perrin (footnote 1), p. lv.
33. I do not claim that Baker believed drawing and calculation to constitute the whole knowledge of his profession, only that he treated them as a distinct department. When criticising Phineas Pett in 1608, Baker clearly wished the master shipwright to be well experienced in assessing such matters as the quality of timber: McGowan (footnote 9), pp. 231-2. For comments on the differences between learning by observation/imitation and via a literate/verbal intermediary, see A.E. Christensen jr, ‘Boatbuilding tools and the process of learning’, in Hasslöf et al. (footnote 17), 235-59.
34. J.T. Leader, Life of Sir Robert Dudley, Duke of Northumberland (Florence, 1895), pp. 56 and 188. Independent evidence of the connection between Dudley and Baker is provided by a brass semicircular instrument in the Museo di Storia della Scienze, Florence. Associated with one of the large Dudley astrolabes (II, 47) in the collection, the semicircle carries a triangular scale of proportions of exactly the same type as appears in Fragments. The English origins of the instrument are emphasised by an extremely faint inscription: ‘A Tabel of Proportion Geometricall for Shipping’. Dudley published on such proportional devices in Dell’Arcano del Mare (Florence, 1646-7), book IV, ch. 5.
35. Pepys Library, PL 2878, p. 493 (a 17th century copy). For the agreement which preceded this request, see PRO SP12/218/31-3.
36. Testimony to the 1608 Commission of Enquiry: McGowan (footnote 9), p. 234, cf. ibid., pp. 236-7.
37. Report of c.1587, printed in John Knox Laughton (ed.), State Papers relating to the Defeat of the Spanish Armada, Navy Records Society (London, 1895), I, p. 39. More generally, see Simon Adams, ‘New light on the "Reformation" of John Hawkins: the Ellesmere naval survey of January 1584’, English Historical Review, 105 (1990), 96-111 and David Loades, The Tudor Navy: an Administrative, Political and Military History (Aldershot, 1992), pp. 184-5.
38. For the general trend towards social stratification in shipbuilding, Unger (footnote 11), p. 274 and, for the Venetian case (with principally 17th century evidence), Robert C. Davis, Shipbuilders of the Venetian Arsenal: Workers and Workplace in the Preindustrial City (Baltimore, 1991), pp. 180-1. For the Venetian Arsenal and its social structure in the 15th and 16th centuries, F.C. Lane, Venetian Ships and Shipbuilders of the Renaissance (Baltimore, 1934) and Maurice Aymard, ‘L’Arsenal de Venise: science, expérience et technique dans la construction navale au XVIe siècle’, in Cultura, Scienze e Tecniche nella Venezia del Cinquecento. Atti del Convegno Internazionale di Studio Giovan Battista Benedetti e il Suo Tempo (Venice, 1987), 407-18.
39. E.G.R. Taylor (ed.), The Troublesome Voyage of Captain Edward Fenton 1582-3, Hakluyt Society, 2nd series, 113 (Cambridge, 1959), p. 154. Note that this separation of responsibility does not necessarily depend on or imply the use of plats, though it is suggestive.
40. The contrast is clearly marked by the title of the first published arithmetical text in English, the anonymous An Introduction for to Lerne to Recken with the Pen or with the Counters (St. Albans, 1537).
41. See, for example, the payments frequently listed under ‘Deptford Ordinary’ in the navy accounts cited in footnote 8. For arithmetic ‘with the counters’, F.P. Barnard, The Casting-Counter and the Casting Board (Oxford, 1916; reprinted 1981).
42. Baker readily incorporated symbols into his work. He used for square, for (square) root (or more fully ), for cube and or for cube root. These symbols can be found in Robert Recorde, The Whetstone of Witte (London, 1557), sigs S1v and Ll3r-v.
43. However, Baker’s usage was not idiosyncratic. ‘Demonstration’ was used in the same sense by mathematical practitioners such as Thomas Hood, The Making and Use of the Geometricall Instrument, called a Sector (London, 1598), f. 9r-v.
44. Baker provided his own template for constructing linear scales. He drew up a device with 60 equidistant parallel lines to divide any suitable line into a given number of equal parts (p. 55). This method is described, for example, in John Blagrave, The Mathematical Jewel (London, 1585), pp. 4-5.
45. Fragments, p. 73. Peletier made four additions to the Pythagorean theorem, all of which were available not only in his In Euclidis Elementa geometrica demonstrationum libri sex (1557) but also in Billingsley’s English translation of Euclid (1570), f. 58v.
46. Alae seu Scalae Mathematicae (London, 1573), sig. K3r. For Digges, Chancellor and the earlier history of transversals, see above, chapter 2, section 2.
47. Hakluyt (footnote 24), V, p. 76.
48. PRO HCA25/1, part 2. The document is one of an unpaginated bundle. Note that the Judith’s official burden was 110 tons (confirmed by PRO SP12/107/68), whereas Borough later described it as of 75 tons (SP12/129/11). The discrepancy is explained by the differing systems of tonnage calculation: deadweight (tons and tonnage) for royal ships, carrying capacity of goods (tonnage) for merchantmen. For tonnage, see William Salisbury, ‘Early tonnage measurement in England’, Mariner’s Mirror, 52 (1966), 41-51, though its account of Baker is not entirely adequate.
49. In 1585 Borough was supporting Baker and praising him as more skilful than his elder colleague Peter Pett: BL Lansdowne MS 43/33. For Borough, see below, chapter 4; for Dover, see chapter 5.
50. Baker: Fragments, pp. 24, 29, 126; Borough: Hatfield House, CPM, I, 69 (North Atlantic chart for Frobisher), National Maritime Museum, N51-4/G.215:1/5 MS (passage from England to the Gulf of Finland).
51. PRO SP12/243/110. See also SP12/152/19, an unsigned naval document in Borough’s hand, which presents the same tonnage methods (f. 49r). (This ostensibly administrative paper also has a remarkable addendum to its prescriptions for ropes and rigging, in which Euclid is quoted on the proportions of circles and a geometrical diagram provided to show the calculation of the area of a circle; f. 51r.)
52. W. Borough, Discours of the Variation of the Cumpas (London, 1581), sig. *3v.
53. The following remarks are based on Jon V. Pepper, ‘Harriot’s manuscript on shipbuilding and rigging (ca. 1608-1610)’, in Derek Howse (ed.), Five Hundred Years of Nautical Science, 1400-1900, Proceedings of the Third International Reunion for the History of Nautical Science and Hydrography (Greenwich, 1981), 204-216 and John W. Shirley, Thomas Harriot: A Biography (Oxford, 1983), pp. 97-103.
54. On Bourne, see the introduction to E.G.R. Taylor (ed.), A Regiment for the Sea and other Writings on Navigation by William Bourne, Hakluyt Society, 2nd series, 121 (Cambridge, 1963).
55. For Bourne’s appointment, Bodl. Rawl. MS A 202, f. 40r.
56. W. Bourne, A Booke called the Treasure for Travellers (London, 1578), III, f. 14r.
57. Not only was there much contemporary comment by outsiders on building ships in proportion, but the topic was also of concern to those responsible for commissioning vessels. Note, for example, that the largest ship agreed on in 1588 (footnote 35) was to be moulded like the earlier Revenge, but 200 tons heavier.
58. Bourne (footnote 56), III, f. 15v.
59. Bourne (footnote 56), III, f. 16v.
60. Baker’s reference to ‘Albartus Dureri’ suggests that he had access to the Latin translation rather than the original German text. For Dürer’s presentation of the cube problem, see Albertus Durerus ... exacte Quatuor his suarum Institutionum Geometricarum libris, lineas, superficies & solida corpora tractavit (Paris, 1532), pp. 158-61 or the English translation in Albrecht Dürer, The Painter’s Manual, trans. W.L. Strauss (New York, 1977), pp. 346-353. The ultimate source for Dürer’s method was Pappus’s Mathematical Collection, relayed through Eutocius’s commentary on Archimedes’s De Sphaera et Cylindro. Dürer did not give a proof of the result. For Pappus’s proof, see P. Ver Eecke (ed. and trans.), Pappus. La Collection Mathématique, 2 vols (Paris, 1933), I, pp. 47-50 or T. Heath, A History of Greek Mathematics, 2 vols (Oxford, 1921), I, pp. 266-8.
61. Compare Dürer’s various spirals, and particularly the curve to be used for towers: Dürer, trans Strauss (footnote 60), pp. 47-51, 85-7, 239-40 and 453-5.
62. Note in particular the appearance of the tale in the English Euclid of 1570, f. 58r. Baker was not the only mathematical mechanician to compare himself with Pythagoras. Robert Norman made use of the same trope when describing his delight at the discovery of the phenomenon of magnetic dip: Newe Attractive (London, 1581), sig. A2v. Indeed, Norman also used the ‘Eureka!’ story of the naked Archimedes to express his own joy.
63. Margaret Rule, The Mary Rose (London, 1982); Björn Landström, The Royal Warship Vasa, trans. Jeremy Franks (Stockholm, 1988).
64. Lavanha’s text, dated by Barata to the first quarter of the 17th century, appears in Barata (footnote 15), pp. 264-294. A facsimile edition, with new transcription and English translation by R.A. Barker, is forthcoming. My thanks to Richard Barker for sight of this translation prior to publication. On Lavanha, A. Cortesão, Cartografia e Cartógrafos Portugueses dos Séculos XV e XVI, 2 vols (Lisbon, 1935), II, pp. 294-361.
65. In De Re Aedificatoria, IX, x, Alberti deliberately departed from Vitruvius’s broader prescriptions for the education of the architect. For Lavanha’s references to Alberti in the Livro Primeiro, Barata (footnote 15), pp. 265 and 267.
66. Alberti had, however, mentioned ships in the context of architecture. In De Re Aedificatoria, V, xii, he noted two ways in which ‘the art of building may contribute to the safety and victory of generals of fleets and their forces: the first consists in the right construction and rigging of the vessels ...’. Alberti went on to name the major parts of a vessel and gave a few proportions before referring the reader to a fuller exposition of such matters in his now lost treatise on ships; J. Gadol, Leon Battista Alberti: Universal Man of the Early Renaissance (Chicago, 1969), p. 204.
67. Livro Primeiro, chh. 5-7. An earlier Iberian discursive treatment of shipbuilding also covered the same range of material topics: Oliveira (footnote 15), chh. 2-4. In the prologue to this text of c.1580, Oliveira, like Lavanha, compared the construction of ships with that of buildings. Significantly, Oliveira was familiar with sources such as Vitruvius.
68. Sig. d4v. Dee’s interest in naval architecture is revealed by a manuscript volume in his library: ‘Naupegia Itali cuiusdam, cum figuris. papyro 4o’. Unfortunately, this evidently anonymous manuscript has not been identified; Julian Roberts and Andrew G. Watson (eds), John Dee’s Library Catalogue (London, 1990).
69. Stratioticos (London, 1579), sig. a4r.
70. PRO Prob 10/305, also in PRO PCC 83 Capell (Prob 11/122).
71. E.G.R. Taylor, Mathematical Practitioners of Tudor and Stuart England (Cambridge, 1954), p. 199.
72. John Wells to Henry Briggs, 9 January 1621 in S.J. Rigaud, Correspondence of Scientific Men of the Seventeenth Century, 2 vols (Oxford, 1841), I, pp. 5-6 and cf. Fragments, pp. 99-100 for earlier references.
73. In particular, the ‘Scott MS’ (Royal Institution of Naval Architects, Scott MS 798), as well as a related text now printed as Richard Barker, ‘A manuscript on shipbuilding, circa 1600, copied by Newton’, Mariner’s Mirror, 80 (1994), 16-29. Also note the anonymous treatise on shipbuilding attributed to John Wells and published by W. Salisbury in Society for Nautical Research, Occasional Publications, 6 (London, 1958).
74. A.H. Markham (ed.), The Voyages and Works of John Davis the Navigator, Hakluyt Society, 59 (London, 1880), pp. 234-6.
75. A.B. Grosart (ed.), The Works of Gabriel Harvey, 3 vols (London, 1884-5), II, pp. 289-90.