The Mathematicians

The juxtaposition of painting and geometry is now familiar and unexceptional in our appreciation of the Renaissance. But problems still arise when this understanding is translated, as it often is, into a supposed congruence, now lost, between art and science, allegedly epitomized by the catholic activity of 'Renaissance man'. It is then that irrelevant modern notions of science and art too easily create confusion and misunderstanding, as though this Renaissance paragon speaks to the modern disjunction between 'two cultures'. Instead we must try for a moment to lay familiar meanings aside and to use these terms, 'art' and 'science', in their Renaissance and early modern senses.

In a Renaissance incarnation we might be told that just as the new science of perspective is reforming the traditional art of painting, so other branches of mathematical science are reforming other useful arts, such as building, land measuring, map-making, navigation, time-telling and so on. By mastering a familiar terminology with unfamiliar meanings, we would come to understand a different relation between the terms 'art' and 'science', whereby certain sciences, in fact aspects of geometry, are the technical foundations for the practical work of respective arts. Science is knowledge of a special kind - certain and eternal - while art shares the uncertain fate of all things material. The particular claim of those promoting the mathematical sciences with increasing vigour and success seems to be that mathematics is relevant to a whole range of arts, where practice would benefit enormously from a refoundation on the science of geometry.

So far, in our Renaissance guise, we have referred to science and to art, but we have said nothing about nature. The fact that we have managed this exclusion is one indication of how far we have moved from the modern notion of science. There was indeed, maintaining Renaissance terminology, a science of nature - a natural philosophy. Traditionally it was an elaborate and sophisticated account, derived from Aristotle and taught in the universities, which presented the causes that lay behind the phenomena of the natural world. Since the work of God in the natural realm was distinct from the work of man, so nature was distinct from art, except as an object of imitation, and separate in turn were their respective sciences - natural philosophy and mathematics. True, there were a few real enthusiasts - Leonardo was one - who seemed to claim that the imitation could be so powerful that the science underpinning these arts might have some claim to be a natural philosophy. It is also true that, shedding our guise, we know that mathematics will come to have an explanatory relationship to the natural world. But how this might happen need not disturb us for now. The message of the picture at the centre of our exhibition - The Measurers - deals with the mathematical arts and the mathematical science of geometry, but it says nothing about nature.

This vigorous mathematical programme - the reform of a range of practical arts through the application of geometry - began as a Western European movement in Italy in the early fifteenth century, particularly in Florence. It flourished through cartography, navigation and astronomy. Its most conspicuous material records derive from the widespread publication of mathematical books and the design and manufacture of mathematical instruments by specialist makers in centres of production established across Europe. A northward movement benefited particularly from the influence of the German astronomer Johannes Regiomontanus (1436-1476), who had close links with Italian mathematicians, and who was responsible for the importance of Nuremberg as a centre of mathematical publication and instrument making. Among the German mathematicians in the tradition of Regiomontanus was Peter Apian (1495-1552), or Petrus Apianus, who has a particular relevance to the development of practical mathematics in the Netherlands.

One of the earliest indications of a Flemish centre for this mathematical movement came with the publication at Antwerp in 1529 of an edition of Apian's Cosmographia (first published in 1524) prepared by the young mathematician Reiner Gemma (1508-1555), born in Friesland and known as Gemma Frisius. Gemma had studied and was now practising medicine in Louvain. His version of the Cosmographia, improved over a succession of editions, was one of the most popular books of the time, and editions and translations appeared throughout Europe in the sixteenth century. In Louvain, Gemma established a workshop for the production of globes and mathematical instruments and he followed a mathematical career typical of the eminent sixteenth-century practitioners, involving the pursuit of astronomy and cartography, the design and manufacture of instruments and the publication of books on a range of topics in practical mathematics. He began producing printed globes in 1531 in collaboration with Gaspar van der Heyden, who was probably responsible for the engraving work, and among Gemma's designs were adapted and improved versions of the astronomical rings (figures 46 and 48) the cross-staff (figure 14), and the universal astrolabe (figures 40 and 42).

A brief survey of the leading Flemish practitioners will convey a picture of the mathematical tradition established by Gemma. His most celebrated pupil at Louvain was Gerard Mercator (1512-1594), born at Rumpelmonde near Antwerp. Mercator entered University in 1530, but his mathematical training with Gemma seems to have been undertaken privately and informally. It may be that he learned the skills of engraving in Antwerp; indeed it is possible that it was the promise offered by Mercator that allowed Gemma's ambitions in practical mathematics to be fulfiled through the foundation of a workshop. Mercator stayed in Louvain till 1552, leaving on account of the religious persecution he experienced as a Lutheran. He was an outstandingly able mathematical practitioner - designing and making instruments, globes and maps, as well as carrying out extensive surveying work in Flanders, where he applied the techniques he had learnt from Gemma. Mercator is, of course, best known through his contributions to cartography.

After Mercator's departure, charge of the workshop in Louvain fell to Gualterus (Walter) Arsenius (fl.1555-1575), nephew of Gemma. He made beautiful and elegant astrolabes, as well as armillary spheres, cross-staffs and astronomical rings. Such was the fame of Gemma and the workshop he had created at Louvain that Walter often signed his instruments as the nephew of the famous mathematician rather than or as well as in his own name.

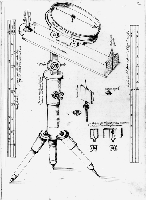An instrument maker who was a friend of Mercator and who modelled his work on the Arsenius school was Michael Coignet (1544-1623), a native of Antwerp, where he spent his working life. It is significant, and typical of the practice of geometry at the time, that although we know Coignet best as a maker of instruments and an engraver of maps, he identified himself in a Latin manuscript now in the Bodleian Library as 'Michaelis Coignęti Mathematici Antverpiani' and is described in an English work of the period as 'Mathematician of Antwarpe'. As well as making instruments, he wrote general books on mathematics. As we have seen with Mercator, the roles of geometer and instrument maker were not sharply differentiated: it is characteristic of Renaissance geometry that these were complementary aspects of a single discipline. Coignet's patron was Albert VII, Archduke of Austria, and it is to Albert that the Bodleian manuscript is dedicated.

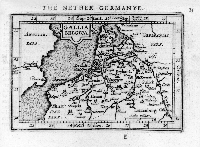Another feature of practical geometry that is already clear is the catholic range of its relevance and application. Cartography, for example, features in the activities of each of the practitioners we have mentioned thus far and is one of the areas of outstanding achievement in the Flemish school. An early figure more particularly remembered as a cartographer was Gerard de Jode (1509-1591), born in Nijmegen and practising in Antwerp. He began producing maps in 1555 and his atlas, Speculum Orbis Terrarum, appeared in 1578. His rival, Abraham Oertel (1527-1598), known as Ortelius, had anticipated him in the production of an atlas when his Theatrum Orbis Terrarum was published in 1570. Ortelius was born, lived and died in Antwerp, though he travelled widely in Europe. He was a close friend and sometimes travelling companion of Mercator, whose own Atlas began to appear in 1585 (it was Mercator who first used the word to denote a collection of maps), and Ortelius referred to Mercator in the Theatrum as 'Geographorum nostri temporis coryphćus' ('the prince of modern geographers'). Mercator is thought to have been influential in Ortelius's choice of career, while readers of the English edition of the Theatrum of 1606 were assured that: " no vaine pleasure, or trifles, pastimes (which commonly are the overthrow of many yongue men) could euer with-draw him from his setled purpose, or alienate his minde from his booke. Yet his greatest delight and commendation consisted in the knowledge of the Mathematicall sciences."

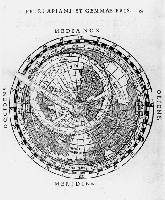Cartography and instrument making share the skills and disciplines of engraving, surveying, navigation, geometrical projection and astronomy. The link is epitomized by an astrolabe included in the exhibition, based on a geographical planisphere rather than a projection of the heavens (figure 36). The design is usually attributed to Apian and a paper version is included in Gemma's editions of the Cosmographia (figure 38).

The celebrated Antwerp printer Christoph Plantin had a role in the careers of most if not all of these practitioners. He collaborated with de Jode, but was particularly close to Ortelius. He sold globes by Gemma and by Mercator, as well as Mercator's maps, and stocked Arsenius instruments such as astrolabes and cross-staffs. Plantin was also a friend of Simon Stevin (1548-1620), a native of Bruges who was a mathematician, surveyor and engineer and who wrote widely in the mathematical sciences, including works on perspective, navigation and astronomy.

Jodocus Hondius (1563-1612) was a Flemish engraver and map-maker who acquired the stock of Mercator's business and who, from his printing press in Amsterdam, issued enlarged editions of the celebrated Atlas from 1606. He also produced celestial globes. Willem Janszoon Blaeu (1571- 1638), born in Alkmaar, was another cartographer and globe-maker whose interests extended to surveying and astronomy. Indeed he worked for a time under Tycho Brahe at the astronomer's famous observatory, Uraniborg, and a large mural quadrant by Blaeu, with features characteristic of Tycho's innovations in astronomical instruments, is preserved in the Museum Boerhaave in Leiden. He acquired the copyright of Ortelius's Theatrum in 1625. Blaeu also published general mathematical books, including the works of Adriaan Metius (1571-1635), who was born in Alkmaar and became Professor of Mathematics and Medicine in Leiden. At the end of our survey of Flemish practitioners we find Metius's books dealing with the familiar range of practical application - surveying, navigation, dialling, gauging and, of course, mathematical instruments.

It is noticeable that the world we have glimpsed in these outlined careers is a small one, in the sense that there are many links and relationships between the practitioners. It would not be difficult to reinforce this network with other connections. Coignet, for example, is thought to have been the source for the profound changes in the 1581 edition of the Cosmographia of Apian and Gemma; he was involved with the 1593 edition of de Jode's Speculum and was responsible for the Epitome of Ortelius's Theatrum.

Also noteworthy are the strong English connections to the mathematical life of the Netherlands. John Dee journeyed to Louvain to meet Gemma and Mercator between 1547 and 1551, when he was anxious to introduce his compatriots to the benefits of mathematical science. He returned with instruments designed by Gemma and made by Mercator. Ortelius reciprocated by visiting England in 1577, and came to know Dee, as well as William Camden and Richard Hakluyt. Hondius worked for some ten years as an engraver in London, along with other Flemish refugees from religious persecution, and he engraved the plates for John Speed's atlas. Most of Christopher Saxton's engravers also were Flemish craftsmen. Coignet engraved the maps for the London edition of Ortelius's Epitome of 1603. Some of Stevin's works appeared in English editions. Finally, perhaps the most important link of all is that the English school of mathematical instrument making, which reached such heights in the seventeenth and eighteenth centuries, can be traced to the workshop founded in London by the Flemish immigrant known as Thomas Gemini (fl.1524-62), who may well have been connected with the workshop established by Gemma in Louvain (see catalogue no. 42).