Chapter 5
DOVER HARBOUR
Constructing design, designing construction
1. HARBOUR DESIGN AND MATHEMATICAL PRACTICE
During the summer of 1583, Dover was the site of perhaps the largest and probably the most intensive construction project of the Elizabethan period. Over the course of a few months, the major phase of a long-planned harbour project was completed: using hundreds of labourers and horse-drawn carts, a seafront area of some 17½ acres was cleared and enclosed within earthen walls. This ‘pent’ was designed to retain both fresh and salt water at high tide and, by means of sluices, control its outflow at low tide. The controlled rush of water would then scour the harbour and clear its mouth of any accumulated shingle and debris.
Faced with the task of overseeing the construction of this pent, the on-site administrators at Dover were confronted with a maze of problems. To maintain control of the process, they had to make (and frequently remake) innumerable day-to-day decisions. From the voluminous surviving documents, the detailed business of the harbour works can be followed on a weekly and sometimes even daily basis. The complex logistics required management of the number of workers and carts, of the [page 219:] allocation of resources, the availability of pasture for the horses, the timely supply of money for wages, the provision of earth and chalk for the walls, and the procurement of skilled artisans for the most difficult and dangerous aspects of the work. Materials, money, labour, time, expertise: the harbour’s pent was constructed from all these heterogeneous elements.
But these were not the only elements necessary to place Dover at the centre of a large-scale construction project. There were two extra prerequisites to the task of construction. First, the highly expensive project had to be championed as a national rather than a merely local venture: before being built of earth, chalk, timber and iron, Dover harbour had to be persuasively presented as an undertaking worthy of state financial support. The promoters portrayed Dover as the ‘eye of the kingdom’, using as their principal argument the town’s strategic location at the narrowest point of the English Channel. Thus, to mobilise state support, Dover had to be rhetorically constructed as a key site for the achievement of military, political and commercial objectives.1 The second prerequisite was for the form and cost of the proposed harbour to be established and agreed in advance. Although the principal and most visible phase of work began in May 1583, an enormous amount of planning and preparation had already been carried out. It is this last aspect of the project, the process of design, which forms the core of my account.
The design process was a lengthy and tortuous one. Beginning as early as [page 220:] 1576, its initial prosecution was faltering and intermittent. However in the early 1580s the number of competing proposals dramatically increased and the resulting options were examined and either endorsed, rejected or merely left to languish in limbo. Nor was the design process complete in 1583, when the pent was successfully achieved. This structure had been only one component of the overall harbour plan and there still remained much else to accomplish. The larger project stretched on into the 1590s and, over the long years of construction, there were frequent alterations and additions to the agreed layout, structure and materials. The process of design thus not only preceded construction but also interacted with it and even sometimes followed it.
The cast of participants featured in the early years of the design process differed markedly from those who were later responsible for construction. Design involved projectors, planning engineers, and practitioners rather than clerks, foremen and labourers. Moreover, whereas construction was overseen chiefly by local gentlemen (with only indirect monitoring by the Privy Council), the Lords of the Council actively intervened in the design process.
Studying the design process means examining the formulation of proposals and the competitive presentation of alternatives and options. It requires us to examine how, by mustering the resources of nature, money and technology, projectors and practitioners transformed personal suggestions into credible plans. The argument of this chapter is that mathematical practitioners successfully deployed a distinctive set of resources to draw up and display their plans for the harbour. I argue that geometry and arithmetic, the two fundamental mathematical arts, were translated into paper resources that could be used to persuasive effect. Geometry was translated into the form of scaled plans and drawings, while arithmetic appeared in the work of financial [page 221:] calculation. The mathematical practitioners mobilised these resources to win technical and rhetorical advantage in the decision-making process. They integrated the visual representations of their drawn plans, their ‘plats’, with calculations to try and tip the argumentative balance in their favour and thus secure the approval of Privy Councillors and harbour commissioners.
For the mathematical practitioners, and indeed for all other participants, harbour design was unusual work. According to Thomas Digges, the new harbour proposed for Dover was ‘a great and strange work’.2 Major harbours were not designed and built in England on a regular basis. Of course, harbours had been constructed before, and other building projects could also serve as models for the enterprise. But there was no corps of established harbour engineers to whom administrators and statesmen could turn. Nor was there a fixed or universally accepted procedure to follow. In particular, there was no widely-held conception of the design process and its constitutive elements. The very term ‘design’ was an unfamiliar one and the mathematical practitioners could not assume that their expertise would be accepted as relevant. So, as well as showing in detail how geometrical plats and arithmetic were used by mathematical practitioners, I also want to suggest that their combined use of these resources helped to construct design as a distinct activity with its own requirements and procedures. Design was not necessarily temporally distinct from construction; on the contrary, it could (and, at Dover, did) continue in parallel. But design did become distinguishable from construction because its medium, its personnel and its social location were differentiated.3 [page 222:]
The mathematical practitioners were thus working on two levels of the design process. On the one hand, they were bringing plats and numbers into the details of technical decision-making, but on a more general level they were also redefining the nature and practice of design itself, and placing themselves at the centre of this new design activity. Moreover, beyond the realm of design, they were consolidating not only their personal and individual credit with the Privy Council but also the role of the mathematical practitioner as a reliable and expert servant of the state.
This chapter considers the design process at Dover in terms of geometry and arithmetic. Following the perceptions of the practitioners, I use these two arts as twin lenses through which to view the surviving material. The practical geometry of plats forms the centrepiece of the chapter but is supplemented and underpinned by the practitioners’ arithmetical skills. After dealing with the use of plats and the function of arithmetic in resolving technological issues, I present a detailed case study of one of the many controversial episodes which flared up during the Dover design process. Numerous recent accounts in the field of science studies have demonstrated that conflict often provides the best ‘way in’ to the presuppositions and strategies of competing sets of actors. Controversies offer the same opportunities to the history of technology. In the case of Dover I show how mathematical practitioners used the resources of plats and calculation to enrol nature, finance and past experience, and thereby challenge and overthrow the claims of a seemingly successful projector. Dover was a site where mathematical practitioners shared common purposes and strategies, and where they laboured to articulate both their role and status. Dover served as a specific site for the creation of a community and its technical practices. [page 223:]
2. ‘A PERFECT AND AN ABSOLUTE WORK’
Before moving on to the primarily thematic and analytic concerns of this chapter, I first want to provide a basic narrative in which later examples can be anchored. After briefly noting the early 16th century background to the Elizabethan works, I outline the development of the Dover project between 1576 and 1585, sketching the design process as well as the early stages of construction. This simplified chronology also offers an opportunity to trace the participation of the practitioners and mechanicians who have already been discussed in previous chapters: Thomas Digges, Mathew Baker, William Borough, Thomas Bedwell, Robert Stickells, John Symonds, Paul Ive and John Hill.4
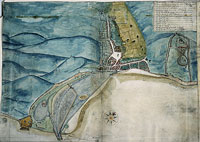
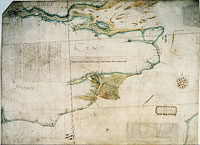
The Elizabethan works were not the first major harbour project at Dover. Indeed, in certain respects, the Elizabethan works were on a decidedly smaller scale than those initiated and executed earlier in the century, during Henry VIII’s reign. [page 224:] While the earliest pier had probably been built around 1500, the principal works began in 1535 and finally tailed off in 1551, a few years after Henry’s death.5 At the close of the Henrician project, Dover town and castle had been provided with a substantial harbour structure (Figure 5.1).
There are two essential points to be drawn from the Henrician works. One concerns the cost of the project, the other its success. On the one hand, the works were quite exceptionally expensive and yet, on the other, the lavish expenditure brought no guarantee of success. By the mid-1550s, despite the huge sums spent, the harbour had completely failed, its mouth blocked by an enormous bank of pebble and shingle which was still there when Digges made his survey 25 years later (Figure 5.2).
This failure was of course a major intellectual and practical problem for the Elizabethan projectors. For sovereigns, statesmen and administrators, Henry VIII’s works taught an alarming lesson: the harbour could be a financial black hole, swallowing immense sums of money with no long term return. Henry’s extraordinary expenditure was certainly well-remembered in the 1580s. As Reginald Scot noted: ‘during the time of all the work, the king’s coffers seemed to stand wide open’.6 For engineers and practitioners, the failure posed an acute problem: why, despite protracted effort, had these ambitious works been utterly negated within a few years of their completion?
There was general agreement on the proximate cause of the failure: the sea had brought in pebble and shingle to choke up the harbour’s entrance. But consensus [page 225: Figure 5.1] [page 226: Figure 5.2] [page 227:] was not so readily achieved on the how and the why of this process. It would be easy, indeed too easy, for the historian to present a simple explanation of the ‘inevitable’ failure of the Henrician project. Drawing on 19th and 20th century experience, we can, if we wish, diagnose the flaws and failures of the early 16th century endeavours. But this approach would offer us absolutely no help in understanding the decisions of the Elizabethan designers. Like the mathematical practitioners themselves, we cannot prejudge the issue and decide precisely what had gone wrong and why. They were faced with the enigmatic evidence of the decayed harbour and with the confusing and often conflicting memories of mariners and townsmen. Thus, in their design deliberations, the reasons for the failure of the Henrician works were crucially at issue.
After the failure of the harbour in the 1550s, there was little positive action for 20 years. The town addressed a series of petitions to the Privy Council calling for renewed investment to restore the harbour, but in vain. Meanwhile, ambassadors occasionally wrote from Dover to the Court to express either irritation or embarrassment at the long delays and hazardous departures which they encountered before their passage across the Channel.7 However, Dover was not alone in its predicament. Other ports on the south east coast faced similar problems and Dover’s efforts to muster support for the repair and renewal of its harbour became just one more voice in a chorus of complaint and exhortation directed at the central administration. The reiterated requests for assistance finally bore fruit early in 1576 when a parliamentary committee was convened to consider the various petitions that had been received from port towns. A commission was subsequently appointed to [page 228:] survey and report on Dover, Rye and Winchelsea; the design process had begun.8
The 1576 commission recommended Dover as the most suitable site for a new harbour. In order to keep the harbour mouth open, the principle of a pent was adopted, evidently borrowed from continental models.9 Plats were prepared but no one had any stomach for the estimated cost of £30,000 and the proposal languished until early 1579 when winter storms breached the harbour walls and required some smaller-scale repair work. The proposed repairs provided an opportunity to revive the larger question of renewing the harbour as a whole, and the town procured a new proposal with a much lower estimate of £16,000. Tempted by this more palatable estimate, but wary lest they be ensnared in a scheme whose costs would rapidly escalate once work got under way, the Privy Council appointed a commission of county notables and local gentlemen to review the available plans. Although noting the new 1579 plan, the commission favoured the original proposal of 1576, which had now been revised to bring its budget down to a more manageable level of £21,000. But though there was now agreement on the proposal’s technical feasibility, finance again proved the sticking point and the scheme remained on paper.10
With progress stalled on the commission’s approved plan, it took a radically different design to restart the process in the summer of 1580. Proposed by John [page 229:] Trew, an experienced engineer and projector, the cost of this new design was reckoned at perhaps £8-10,000. Though it won the all-important approval of the Privy Council, the promise of an affordable new harbour did not overcome their financial prudence: they ordered the building of a trial section of wall in order to establish a reliable estimate of unit costs. The preparatory stonework for this test piece continued over the winter while, in early 1581, the future of the project was apparently secured through the creation of a new funding mechanism: an act of parliament which raised a 7 year levy on ships to provide the money for the harbour.11 However, despite the appearance of technical and financial closure, there were simmering doubts over the feasibility of Trew’s scheme. These concerns came to a head in the summer of 1581 when Trew’s plans and practice were reviewed and found wanting. Suddenly, from being a successful scheme in full flow, the works were brought to a standstill and planning began once again from scratch.12
Between the autumn of 1581 and the spring of 1582 there was an explosion of new proposals which a fresh commission examined in April 1582. Although the commissioners recommended their own solution, the Council decided that a cut should first be made through the seaward bank of shingle currently blocking the harbour. This cut would not only establish a new (though temporary) harbour mouth but would serve to drain the harbour so that the current disposition of shingle, mud and sand could be more accurately ascertained. Preparations for the cut were made over the summer and autumn of 1582, though the work itself was not carried out until the difficult winter months of December and January. [page 230:]
The draining of the harbour did not automatically create consensus amongst the various disputants. Indeed, the level of debate and the number of proposals continued to escalate and reached a crescendo in March and April of 1583. The overall form of the harbour was still at issue and the commissioners reasserted their conviction that their own proposal was the most likely to succeed at reasonable cost. Since it was intended to employ the farm labour traditionally free between harvests, time was now beginning to run out and, with the threat of another major delay to the project, opposition to the commissioners’ plat was finally silenced.
But even if agreement could be secured on the question of the harbour’s overall layout, there was still vigorous debate on more detailed questions such as the appropriate form and materials for the walls of the pent. Many proposals, drawings and models were submitted but, after an intensive period of consultation in London and Dover, the Council (at Lord Burghley’s instigation) opted for a tried and tested method. Despite competing proposals for walls made of wood or, more cheaply, of ‘slub and sleech’ (the mud available in the harbour), the technique chosen was that of reinforced earthwork, as traditionally employed at Romney Marsh, along the coast from Dover.
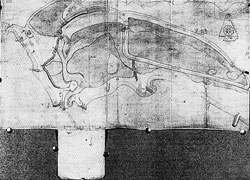
Over the summer of 1583, the pent was constructed and equipped first with a temporary and then a more permanent wooden sluice (Figure 5.3). But much work still remained to be done. Attention now turned to the provision of a new mouth for the harbour. As with the issue of the pent walls, the question of the position and form of the harbour mouth blew up into a major controversy. Although soundings were taken in December 1583 to establish the disposition and nature of the seabed, the debate continued until June 1584, involving knights, navigators and local mariners. [page 231: Figure 5.3] [page 232:] Once agreement was finally reached, the labour of clearing the chosen spot began and work proceeded at and around the harbour mouth during the remainder of 1584 and in 1585.13
During the same period a variety of groynes, jetties and walls were constructed and repaired, as the sea continually eroded and destabilised sections of the shingle banks on which the harbour walls stood. But at this stage, leading into 1586, the major stages of the work were complete and Reginald Scot felt able to enthusiastically proclaim the harbour as ‘a perfect and an absolute work’.14
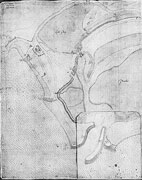
Scot’s enthusiasm was no doubt deemed appropriate for a public description and celebration of the project. But the harbour was far from perfect. Extra groynes were built and, during the 1590s, additional walls and a new sluice were constructed; the harbour mouth was also remodelled (Figure 5.4). However, from the point of view of the design process, the major activity took place in the period from 1576 to 1585. During this critical decade the various practitioners and mechanicians each played differing roles depending on their status and expertise.
The gentleman and mathematician Thomas Digges was on the 1576 parliamentary committee which led to the original survey of the harbour.15 He next featured five years later in 1581 when he was instrumental in halting the work on John Trew’s scheme of 1580.16 Between 1581 and 1584, Digges was one of the most [page 233: Figure 5.4] [page 234:] active and esteemed combatants in the design process. He was made a commissioner in 1582 and appointed to the post of surveyor of the harbour (though other business led him to delegate his responsibilities).17 Digges remained in the role of consultant rather than a supervisor of construction, shuttling back and forth between London and Dover, preparing plans and often pugnacious memoranda, initiating enquiries and consulting with the Privy Council.
William Borough, navigator and Navy official, fulfilled a similar role, though on a rather less elevated social plane. He was on the 1576 commission and seems to have been its principal member.18 (Digges was on the parliamentary committee rather than the commission that was sent out to do the work.) In 1579 Borough was promoting his 1576 plan in its cheaper, revised form and he continued to advocate modified versions through into 1583.19 Although he did not initially resist Trew’s proposal in 1580, he subsequently prepared an important and lengthy paper which sought to undermine Trew’s credibility.20 Borough was often bracketed with Digges as a principal English consultant, and they frequently travelled together between London and Dover.21 Nevertheless, Borough and Digges often squared up on opposite sides of controversial design issues. Digges had initially supported a coffer dam construction for the pent’s walls but in 1583 he switched allegiance to the Romney marsh method; in contrast, Borough was a partisan of wooden walls in 1583.22 Later, in 1584, Borough advocated one location for the harbour mouth, [page 235:] while Digges championed the major alternative.23 Borough’s principal involvement in the project ended in 1584, but he does reappear briefly in the harbour accounts for 1593-4; throughout this lengthy period of service Borough was always a self-consciously independent expert.24
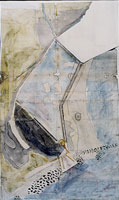
Another member of the original 1576 commission was the royal master shipwright Mathew Baker.25 Although involved at the very beginning, Baker played a much less prominent part in the critical design debates than either Digges or Borough. With his master shipwright colleague Peter Pett, Baker was responsible for the ultimately unsuccessful proposal to build the pent walls of timber.26 However, in 1583 he and Pett secured the contract to construct a wooden sluice for the pent (Figure 5.5).27 Baker was thus involved in detailed design decisions for components of the project, but he was not a major player in the definition of the overall project itself.
Whereas Digges, Borough and Baker had all dealt with Dover in 1576, Thomas Bedwell, the academically educated mathematical practitioner, came to the project later. He submitted his first proposals in spring 1582 when both the overall layout of the future harbour and the nature of the pent walls were at issue.28 In addition to developing his own plans, Bedwell calculated comparative unit costs for [page 236: Figure 5.5] [page 237:] the other schemes and techniques currently being touted.29 But as well as contributing plans and costings in the spring of 1582 and 1583, Bedwell also took on a more administrative role. During the summer and autumn of 1582 he helped to coordinate the provision of supplies and over the winter he acted as a supervisor when the cut was made to drain the harbour.30 However, Bedwell’s involvement at Dover was relatively short: he seems to have left even before the main works began in May 1583.31
The other mechanicians and practitioners were involved in more limited roles assigned later in the project. John Symonds, who was at home as either architect, mason or joiner, was first consulted in the summer of 1583 on the possibility of constructing a stone sluice for the pent, but he advised that it would take too long.32 Nevertheless he was employed again at the end of the year, sounding depths within and around the harbour.33 Other tasks at this time included estimating quantities of materials and drawing up plans, while in September 1584 he was called in to confer on the design of jetties and the suitability of different types of local stone for the purpose.34
Another participant in this conference on jetties and stone was Robert Stickells. Stickells, an intellectually ambitious mason, had first been sent to Dover by Digges in June 1584.35 He was charged then with clearing away the rocks which [page 238:] obstructed the newly agreed location of the harbour mouth. Aside from consulting on stone, he was appointed a ‘work-master’ in autumn 1584 with responsibility for the groynes and jetties at the harbour mouth.36 For a time, Stickells had Paul Ive as a colleague; while Stickells worked at the harbour mouth, Ive was employed as the work-master in charge of building two groynes to stabilise and increase the long bank of beach. Although Stickells stayed on at Dover into 1585, Ive, the peripatetic expert on fortifications, was only present during the latter half of 1584.37
Finally, it is worth noting the last of the practitioners treated in the previous chapter, the auditor John Hill. Hill acted as a local administrator and was particularly active from late 1584 to the end of 1585. He kept Principal Secretary Walsingham regularly up-to-date on the progress of the works, with accounts of successes and failures, and estimates of materials, time and other resources.38 Hill remained active in the running of the harbour works into the 1590s, signing the annual accounts as auditor. But his early responsibilities in the mid-1580s were only those of liaison and co-ordination; he did not take part in any design discussions.39
This review of the practitioners’ activities at Dover omits many of the other important participants, not to say the small army of artisans and labourers. If we were to consider only the larger network of those involved in the design process we would need to look at several more groups and individuals: those lords of the Privy Council who assumed ultimate responsibility for the project; the gentlemen commissioners who [page 239:] deliberated at Dover; John Trew, the engineer who saw his works cut short in 1581; the entrepreneur Fernando Poyntz who, although he repeatedly offered to undertake the works as a speculation, had to make do with more limited tasks such as the execution of the cut during the winter of 1582-3;40 John Stonham, the carpenter from Rye who was entrusted with various parcels of work at Dover;41 and a changing company of ‘strangers’ from the Low Countries (particularly Flanders), who were acknowledged as experts in waterworks.42
The mathematical practitioners form a sub-group of this larger network of design participants. It is, however, striking that only the most sophisticated and committed of the practitioners played a prominent role in the major debates on the general form of the harbour. The more marginal characters such as Symonds, Stickells, Ive and Hill worked within an agreed overall design, occupying themselves with detailed planning and execution. Baker, the most mathematical of contemporary mechanicians, was, like Borough, called in as an expert right from the beginning of the works. But afterwards, like the other mechanicians, he became primarily concerned with specifying detailed components of the overall system. It was the more socially elevated and intellectually engaged group of Digges, Borough and Bedwell who worked on the hierarchically higher level of the overall design itself. Through their efforts they fashioned a design role distinct from the supervision of construction. It is to the constitution of this design role that we can now turn. [page 240:]
3. PRACTICAL GEOMETRY, PLATS AND DESIGN
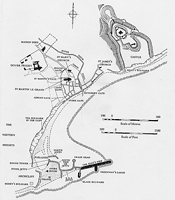
The most visible traces of design at Dover lie in the surviving drawings. Numerous plats (to use the contemporary term) were produced during the harbour project. There are at least eleven surviving Elizabethan depictions of all or most of the harbour, as well as a number of detail drawings showing jetties, wall sections and sluices. Moreover, on the basis of references in surviving documents, it is clear that many other plats were drawn up at the time.43
From the very beginning of the Elizabethan works, plats were identified as important elements in the design process. (Indeed, plats were already being prepared in connection with the Henrician works earlier in the century.44) When the Privy Council charged the 1576 commission with their task of surveying and reporting on the harbours of Dover, Rye and Winchelsea, the Council specifically asked for ‘perfect plats to be made of these particular places mete for the havens’.45 There was thus no debate over the use of plats; they were required and accepted as an appropriate medium for recording information and presenting proposals. [page 241:]
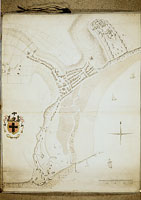
However, although there was acceptance of their use, there were no guidelines or universal conventions governing the preparation of plats. They could (and did) look very different and were deployed for often subtly different purposes. The most vivid contrasts in appearance can be seen when the plats of Elizabethan mathematical practitioners are compared with those of the 1530s (compare Figure 5.6 with Figure 5.2 and Figure 5.3). The practitioners offer vertical plans with prominently displayed scales (or almost vertical bird’s eye views); the 1530s plat provides a quite different representation. Attributed to one of Henry VIII’s painters, the Neapolitan Vincent (Vincenzo) Volpe, it offers a perspective of town, castle and proposed harbour, treating them as the material for a pictorial showpiece.46 The image displays events and topographic detail rather than measured dimensions: note the care given to the representations of the ships coming into the harbour, of the town buildings and castle, and of the cannons sounding out from fortified towers. Particularly striking are the sluices in the centre of the picture, which are of the hand-operated guillotine type. Despite being more distant than the churches in the foreground, the sluices appear larger than the church spires. This is not accident or mistake: the sluices have been drawn extra-large because they are an important part of the harbour proposal. If shown accurately in perspective they would be so reduced in size that their detail would be lost.
A similar, though less marked, contrast can be seen when the Elizabethan practitioners’ plats are compared with those produced by non-mathematical contemporaries. For example, John Lucas, a jurat and mayor of Dover, was responsible for drawing up a plat to represent one of the town’s own harbour [page 242: Figure 5.6] [page 243:] proposals.47 Lucas’s plat, almost certainly from the mid or late 1570s, is again a stylised view rather than a plan. As a ‘perspective’ view we would not expect a scale, though it does note a few important dimensions. What is striking about this plat, with its neatly drawn ships, is that it drastically reconfigures the existing topography of the harbour and magically dispenses with the Henrician works.
It is vital that the contrast between the different types and styles of plat be properly understood. The temptation to fall back on an asymmetric interpretation must be resisted. Volpe’s plat might traditionally be given careful analysis to reveal its pictorial emphasis and representational conventions (for example, the relation between the importance and size of the sluices). Similarly for Lucas. By contrast, the practitioners’ plats would be seen as the unproblematic products of measurement. What indeed could be said about such plats, which would seem to offer a transparently modern window onto the world? Yet the virtues of measurement were not so firmly established in the 16th century as they are now. We are faced not with a polar opposition between the products of artists (such as Volpe) on the one hand and mathematical practitioners (or even ‘scientists’) on the other, but rather with competing and distinct types of cultural artefact. We therefore need to give just as detailed an analysis of the practitioners’ successes as we might do of Volpe’s apparent ‘failings’.48
At issue are the questions of why the practitioners’ plats became the successful ones, and how they became embedded in the process of design. We need [page 244:] to see how they were used, what advantages they conferred, and how they could assist one person or proposal in the face of competitors. In order to tackle such strategic uses of plats, I want to begin by discussing the way in which the practitioners’ plats were prepared; by starting here we can see how their plats were rooted in measurement and practical geometry.
The practitioners helped to make Dover a principal site for the culture and values of measurement. During the planning of the project, basic surveying work was required to generate the diversity of plats and proposals. To estimate the length (and therefore cost) of the various proposed walls, measurements were taken within and across the existing harbour. Unfortunately, there is almost no surviving evidence of the detailed measurement techniques used in this aspect of the design work; rather than the procedures, we have only the products, the plats themselves. However, once recorded in the form of plats, these measurements of length could also serve for the calculation of areas. One of the plats prepared during the most intensive period of design debate in 1582 and 1583 carries notes of the areas of different pent and harbour configurations.49 And once the pent was actually constructed, a ‘perfect measure’ was commissioned in July 1583 which, among other results, determined the area of the various parts of the harbour.50
Aside from the establishment of distances and the calculation of areas, other forms of surveying were carried out. Soundings were taken to determine the profile of both the harbour bottom and the seabed in the bay. For example, Thomas Digges [page 245:] reported that at Dover he himself had ‘seen and sounded all the channels, shelves and roads [roadsteads] there, and set them down exactly in plat’.51 Figure 5.2 (above, p. 227) shows some of these soundings in and around the harbour. More soundings were taken around the harbour mouth in December 1583 by the mason John Symonds, the shipwright Peter Pett and one of the commissioners, Edward Boys. By measuring the depths they set out to establish the size (and relative cost) of the jetties stipulated by the two major alternatives then being considered for the new harbour mouth.52
Beyond the techniques of land and hydrographic surveying, Dover was the venue for extensive quantity surveying. There are innumerable references to the dimensions of planned jetties, walls and other structures. Nor was this numerical work restricted to proposals alone: measurements were frequently taken of features which had actually been built. For instance, the survey of July 1583 (referred to above) established the different lengths and cross sections of the pent walls. Again, the wooden sluice for the pent, having been first planned, drawn and constructed by Mathew Baker and Peter Pett, was then examined and measured in late 1583 by the carpenter John Stonham.53 At the end of 1583, Pett also travelled to Folkestone quarry with John Symonds to quantify the requirements for stonework. They ordered local masons to square off a foot of stone and then hired labourers to carry the piece to town in order to weigh it and thus estimate the number of (cubic) feet in a ton.54 A final example: in 1584 the auditor and practitioner John Hill, by then based at Dover, was charged with taking ‘the breadth, height and length of the stone work [page 246:] already begun there’.55
Through the paper media of plats and records, the practitioners were able to accumulate, combine and muster together these diverse forms of measurement. Plats epitomised the labour of practical geometry, abbreviating its results and drawing them together to create coherent, manageable, and informative artefacts. However, my emphasis on measurement should not be mistaken. In the modern world, measurement is often unselfconsciously seen as a neutral, value-free domain. I want to argue on the contrary that the practitioners’ plats exemplify and proclaim the very values of mensuration itself. Plats are cultural documents which make specific claims for the validity, worth and power of measurement. Far from being just simple bearers of information, the practitioners’ plats are highly charged with meaning and purpose; they interweave what we can (perhaps artificially) distinguish as functional and symbolic realms.56 The historian’s problem is that we are thoroughly imbued with the conventions and values of such representations. Far more work is therefore required to recover the purposive and symbolic dimensions of practitioners’ plats than is necessary for a pictorial plat such as Vincenzo Volpe’s.
To demonstrate how plats represent cultural and symbolic claims as well as physical features and proposed structures, I will examine one of the most important (though enigmatic) of the Dover plats (Figure 5.7). It is probably either by (or based on an original by) William Borough and, if so, represents the form of harbour first recommended by the 1576 commissioners and then subsequently advocated by [page 247: Figure 5.7] [page 248:] Borough until at least 1582.57 Although its rolling hills and perspective representations of buildings give the impression of a bird’s eye view, the plat actually appears to be one of those characteristically Elizabethan productions, a vertical plan to consistent scale with superimposed pictorial detail.58
However, I want to focus here not on the overall format of the plat or the layout of its harbour proposal, but on the seemingly innocuous table in the top right hand corner. The table is titled ‘The true height of certain places above the level of full sea mark’ and it communicates a number of subtle messages to the viewer.
First, consider how the heights of the listed features would have been ascertained. We can quickly dispense with the idea that this might have been by direct measurement. Who would have readily climbed up to ‘the top of the highest chimney in her Majesty’s lodging’ in the castle, while carrying a chain or a rod? Moreover, how could the height of a church’s remains be directly found when they were sitting on top of a hill positioned behind 150 foot high cliffs? It seems clear that the heights were measured indirectly, using the instruments of mathematical practice.
The determination of such heights was a problem made familiar through a wealth of textbook examples dealing with all manner of towers, buildings and other [page 249:] landmarks. Textbooks such as Leonard Digges’s Pantometria (1571) spelled out a range of related procedures, instruments and calculating techniques for finding heights, depths and distances. The plats’s table was evidently prepared by someone familiar with this literature and adept with mathematical instruments and arithmetical calculations. The seemingly inconsequential table already tells us that its author was a mathematical practitioner. (Moreover, the use of fathoms as units strongly suggests a mathematical practitioner with navigational experience.)
What of the table’s purpose? Why would the heights of surrounding landmarks be of interest when the form of the harbour was under consideration? As we will see, it is possible to reconstruct an ingenious, ‘practical’ reason for the table’s presence. But, as a working technique, it would have been impossibly inaccurate. The table therefore served more as a symbol of practice than as a resource for actual instrumental operations. Its use was to celebrate and communicate the values of mathematical practice.
In principle, the table enabled observers to locate their position at Dover, with only a single measurement of elevation and a compass bearing. Although the procedure could have been used anywhere in the harbour, whether on the pier, shingle bank or elsewhere, it would have been especially adapted to a practitioner out taking soundings in a boat. At each sounding, one of the designated landmarks would be observed and, when it came to marking the sounding depths on a plat, the observations could be used to generate a position for each sounding. Given the height of the landmark and the observed value of the elevation, it would only be a matter of calculation to determine the distance of the observer’s position from the landmark.59 [page 250:] With the addition of the relevant compass bearing, the location could be determined on a scaled plat carrying a compass rose.60
However, although the table and its technique were reliable in principle, they would not have been terribly accurate in practice. The landmarks are not particularly high so, if an observer is at a considerable distance, the subtended angle will be very small. For example, the lowest of the landmarks is only 5 fathoms (30 feet) high. This monument would subtend an angle of only 0.65° at a distance of half a mile. Even the highest tabulated point (75 fathoms = 450 feet) subtends an angle of only 9.7° at half a mile. As sensitivity to instrumental and observational error will be greatest when the angle of elevation is small, a practitioner would not have obtained very precise results using this procedure.
So, the table’s appearance of utilitarian functionality is compromised. What, therefore, is the table doing on the plat? I suggest that it encourages us to read and interpret the work as a product of mathematical practice, and to judge it accordingly. The table reminds us that the plat belongs to the culture of practical geometry and measurement. The presence of the table ensures that this plat is distinguished from other, pictorial plats such as those of John Lucas or Vincenzo Volpe (Figure 5.6). Ultimately, this differentiation is premised on a claim for the value(s) of the visual and instrumental resources employed by the mathematical practitioners. [page 251:]
The plats prepared by practitioners thus communicated subtle and persuasive messages to their users. Content and visual appearance were bound up within larger communicative purposes.61 How were such plats actually used in the course of the Dover project? And what features of their plats did practitioners accentuate and exploit to derive maximum advantage in the competitive scramble of the design process?
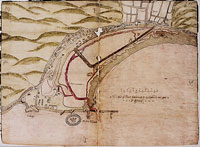
As bearers of the instrumental values of measurement, plats became powerful tools for the mathematical practitioners. To take Vincenzo Volpe’s pictorial plat as a point of contrast once again, we can say that the practitioners’ plats came to be treated as powerful documents because they established reliable two-way relations between the paper artefact and the features of the harbour. A scaled plat simultaneously bound itself to the topography that it represented, and also enrolled that topography as a warrant of representational validity. This is not a simple-minded claim that the practitioners’ plats were more ‘realistic’ than that of Volpe. On the contrary, the ‘optical consistency’ of the scaled plats was such that what was real could be freely mixed with what had only been planned: the achieved and the projected were visually indistinguishable.62 Figure 5.8, for example, shows the form of the harbour mouth as it was in the later 1580s. With no more than a flick of the wrist, the practitioner can flip the double-sided flap to conjure into existence a new harbour mouth which appears just as plausible and real as the existing form [page 252: Figure 5.8] [page 253:] (Figure 5.9).
The dividers surmounting the scale in this plat remind us that dimensions can be either read off or placed on these plan views. Provided with a scale, the plats could be used independently of their original purpose; they could be used to experiment with the harbour in miniature. For example, one could measure the length of proposed walls and compare the cost of building them using different materials and techniques. Scaled plats thus facilitated the comparison of proposals; with a little bit of arithmetical work, different plats drawn on different scales could be quantitatively calibrated and compared.
Practitioners were indeed anxious to compare their plats with opposing proposals in order to highlight the perceived advantages of their own schemes. Thomas Digges, for example, almost always used the current leading alternative as a counterpoint when presenting his proposals for the harbour. While first developing his own ideas in 1581 and early 1582 he sniped at the plat prepared by Flemish ‘strangers’, whereas in 1583 his target was the scheme being promoted by the entrepreneur Fernando Poyntz.63 Again, in 1584, when the form and location of the harbour mouth was under discussion, he sharply polarised the options and vigorously defended his own preference while attempting to demolish the opposition. Digges was perhaps the most self-conscious, aggressive and thorough-going of the practitioners in pursuing this tactic, but it was also employed by others. Borough tackled various Flemish plats of the late 1570s and early 1580s, and he battled with John Trew’s radical scheme of 1580. Moreover, from 1582 to 1584 he was embroiled in all of the major debates, weighing in on one side or the other, undercutting alternatives and [page 254: Figure 5.9] [page 255:] bolstering his favoured options. Likewise Thomas Bedwell, when setting up his own scheme, was careful to differentiate it from others such as those of Digges and Poyntz.
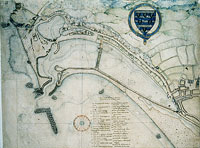
Throughout these long-running arguments, plats were used as crucial resources in attack, defence and compromise. But not only separate and opposing plats were compared; the practitioners also combined comparisons within a single plat. Already, we have seen how a ‘before and after’ scheme could be convincingly presented (Figure 5.8 and Figure 5.9). In at least one instance, a single plat was used for the ambitious task of comparing much larger alternatives for the future form of the harbour. The juxtaposition of Figure 5.10 and Figure 5.11 reveals a flap covering about half the area of the whole plat and intended to present two radically different options for the pent. Such experimentation with alternatives offered a graphic aid to decision-making, while in this case coming close to the limits of the material strength and durability of the paper medium.
This particular plat, probably by Thomas Bedwell and dating from 1582, displays several further extensions of the sophisticated repertoire of paper-based visual techniques.64 On close examination, the harbour mouth is recorded as a pasteover revision, with the original version peeping out from under the lower left hand corner (Figure 5.12). Carefully unglued, the much more substantial (and therefore more expensive) underlying proposal can be seen (Figure 5.13). Even after revealing one layer we do not reach bedrock: underneath this pasteover, there is a further, much [page 256: Figure 5.10] [page 257: Figure 5.11] [page 258: Figure 5.12] [page 259: Figure 5.13] [page 260:] smaller pasteover covering the very narrowest point of the harbour mouth.
The same device of attaching pasteovers to revise details of the proposal was also used elsewhere on the plat: the structure represented at the tip of the large flap was revised with a pasteover. The original wall layout can be seen just above the original harbour mouth in Figure 13; the revised walls are visible just above the revised harbour mouth in Figure 11 (note the shadow above what has now become a flap rather than a pasteover).65
Thus this plat reveals itself as the residue of extensive revision, and it suggests a background of negotiation and debate. It records the technical development of proposals and implies the financial constraints under which they were assessed. Compared to building in timber and stone, paper plats were flexible working tools. Modification and experimentation were possible at relatively low cost before permanent investment was made in physical structures. Practitioners who could master and exploit the paper medium of plats could therefore exert some leverage over competitors in the design debates of the 1570s and 1580s.
The use of plats was not restricted to the development and presentation of options. Even once agreement had been achieved or imposed, and attention had shifted from design to construction, a role was still found for plats. In the summer of 1582, when it was decided to drain the harbour site by making a temporary cut at [page 261:] the mouth, plats were used to provide a contractual record. After agreeing with the Lords of the Council on the work to be done, two plats were drawn up to seal Fernando Poyntz’s contract. The cut was labelled A on the plat, and a possible later extension to the full harbour indicated by an outline marked BCDE. One copy of the plat was signed by Poyntz and retained by the Lords, while the other was signed by Principal Secretary Francis Walsingham as Poyntz’s own record.66
The plats’ visual potential for precise monitoring and control was exploited in the following spring when Poyntz was called to account for his labours over the winter. As the Dover commissioners reported to the Lords on 7 March 1583, ‘there is by Mr Poyntz a cut made somewhat nigher to the pier than in his plot’.67 Writing in the third person and trying to defend himself against criticism, Poyntz had to concede that he had altered the agreed layout: ‘the cut marked A whereby to drain the water he hath made, but hath somewhat altered the channel to the sea ward for the better repulsing of the beach’.68 Plats were not just for the creation of options but could be used to oversee subsequent action.
So far, my focus has remained tightly on the plats themselves as instruments of design, presentation and control. For the practitioners, they were powerful tools. But plats operated and were inscribed within a context of social relations, and they were integrated with other elements of the design debate. To understand the utility and power of plats, they need to be considered not just in relative isolation but as a central element in the mathematical practitioners’ network of resources.69 To [page 262:] complete my discussion of the uses of plats, I will briefly sketch some aspects of this network, to emphasise the heterogeneous character of plats’ affiliations. Not only people and social relations, but also language and material devices such as models were correlated and connected by the practitioners.
The ambiguous contemporary reference of ‘plat’ to both pictorial and verbal documents is troublesome to historians. But it is symptomatic of the close links between visual and verbal proposals. Plats were valuable precisely because they were not used in isolation but could complement and extend verbal justifications of feasibility and cost. An anonymous document puts the point aptly. It discussed the placing of cross walls and bays in the area in front of the town, ‘which upon the plat may best be showed and without ocular demonstration cannot so well by words be conceived’.70
Plats were intended as a concrete point of reference for spoken presentation and discussion, and could be used to abbreviate or avoid otherwise lengthy written descriptions.71 However, while they could on occasion avoid the need for written words, plats were more often securely bound to verbal documents. Thomas Digges was the preeminent exponent of the argumentative strategy which combined text and image; his papers and proposals are studded with phrases such as ‘as in the plat may best be conceived’ and ‘as in the plat is best perceived’.72 But he was far from [page 263:] alone.73
However, the practitioners who artfully integrated text and image did not blindly believe in the universal efficacy of visual representation. (And neither should the historian believe that a plat by itself automatically confers argumentative advantage.) It was indeed their most adept users who on occasion found plats inadequate for their present purposes. For example, Digges, in a paper on the proposed location of the harbour mouth, remarked that ‘the plat without view and trial at the place much abuseth, for the ground shelveth and sinketh downward from the shore eastward down to the Mole, and not southward as by the plat a man would suppose’.74 Digges normally trusted that reliable relations could be established between paper plat and harbour site. However, in this particular instance, he was arguing that the two dimensions represented on the vertical plan view suggested an improper three dimensional profile. For Digges, a plat could therefore be too suggestive and, in this case, he tried to rule out any inference or interpretation which might undermine his own harbour mouth proposal.
Practitioners could therefore not rely on plats as perpetually faithful allies. Although they were the most flexible and frequently used of material resources, additional devices were mobilised when plats were the weakest point in an argumentative chain. Models were the principal supplement to the paper medium of design.
No models survive from the Dover project and their existence is known only [page 264:] from documentary sources. Again, as with ‘plat’, we are plagued by the ambiguous reference of the term: ‘model’ could refer to a diagrammatic drawing on paper as well as a three dimensional physical artefact.75 Thus Digges’s frequent citations of models in his ‘Discourse’ addressed to the Queen may actually have referred to detailed diagrams.76 The character of various other models is also uncertain.77 However, it is certain that not all models were on paper. In some instances a model’s material reveals the nature of the artefact. The harbour accounts for 1582-3 record payment to a Folkestone quarry owner ‘for making a model of stone for Mr Digges all to the use of the said harbour’.78 Moreover, Digges was not the only one to bring physical models into the design process at Dover. Wooden models were used by Mathew Baker and Peter Pett during the controversy over the nature of the pent walls and it seems likely that the carpenter John Stonham also made a wooden model.79
With the occasional aid of models, plats captured and presented both the practitioners’ proposals and also the harbour site itself. Enroling structures, schemes and the ground itself was one achievement. But how did the practitioners use plats to capture the interests and favour of the people who populated the Dover design [page 265:] process?
The practitioners were just one group in the social network which designed Dover harbour. They worked with, and sometimes against, a range of other participants: the Privy Council (based primarily at the Court); the gentlemen and county leaders of the harbour commission (who met at Dover itself); the other entrepreneurs who offered their services; the townsmen and mariners of Dover who were consulted for their opinions and advice; and the specially summoned mechanicians whose skills seemed particularly appropriate. However, everyone accepted that ultimate authority within this diverse assembly rested with the Lords of the Council.
The Council wished to choose a harbour proposal that had been seen, discussed and approved at the site itself. But this raised a problem since, as the chief executive arm of the state, the Council simply could not create the time to visit Dover en masse for extensive design deliberations.80 How could the design process be managed so as to prevent a repeat of the eventual disaster of Henry VIII’s harbour works? Plats were allocated a crucial role in this process of remote control: if the Council could not come to Dover, then Dover had to come to the Council.81 Establishing their visual productions as reliable ambassadors for the harbour privileged the practitioners’ position in debate. They were accepted as providing the most [page 266:] faithful representations not only of the current form of the harbour site but, by extension, its future form as well.
Proposals as well as current matters of fact could thus be presented and evaluated using plats. Plats indeed constituted a technology of ‘virtual witnessing’, to use the expression coined for Robert Boyle’s literary techniques.82 Just as the readers of Robert Boyle’s works would later become virtual witnesses of his pneumatic experiments, so the Lords at Court were able to witness and assess Dover and its projected harbour. Boyle laid particular stress on an appropriate literary form for the presentation of experimental matters of fact. I have emphasised the greater importance for Dover of an appropriate visual form. Nevertheless, plats were often used in conjunction with textual documents (see above). Moreover, the Council made use of an independent apparatus of memoranda, questions, and articles to obtain information from the commissioners and monitor the progress of the works. Exchanged between Dover and the Court, texts could represent the site itself or the views of various participants. Digges, for example, obtained a written record of the responses of Dover mariners to his questions (along with their authorising signatures or marks) and used their now conveniently portable testimony as a ‘touchstone to try and certainly by reason to examine the probability of all plats offered’.83
Word and image thus both played a role in the process of ‘virtual witnessing’. Indeed, we can extend the analogy with Robert Boyle’s 17th century practices. Boyle established experimental matters of fact not only through his ‘literary technology’ of virtual witnessing; he also made use of the material technology of [page 267:] instruments and their operation, and helped to devise a ‘social technology’ for defining and regulating a community of credible practitioners. Likewise, we can complete this account of the practitioners’ plats by reviewing the material and social realms within which both plats and practitioners worked.
The material work of design revolved around the current harbour site and the options for its future development. The practitioners used mathematical instruments and measurement procedures to prepare reliable plats and draw up plausible proposals. When judged necessary, the resources of instruments and plats could be augmented by additional physical artefacts such as models. Indeed, although the material labour of construction remained distinct from design, the choice of building materials came within the scope of the design process and we find even pieces of stone being sent up from Dover to the Court.84
What of the social conventions governing the regulation of credibility and personal credit, and the establishment of the boundaries of design practice? In order to successfully press their claims and advocate their proposals the participants in design had to secure the trust of the Privy Council and the Dover harbour commissioners. Personal credit was intimately linked with technical credibility, and the loss of one would imply the loss of the other. So, for example, when rumours began to circulate that Fernando Poyntz’s attempts to open a cut to drain the harbour had not met with complete success, Thomas Bedwell moved quickly and vigorously to disassociate himself from Poyntz’s work.85 In response to the accusation and [page 268:] gossip, Poyntz made continued efforts to maintain his credit.86 Likewise, any attempt to besmirch Digges’s name and reputation met a forceful response.87
All participants thus aimed to be accepted as trusty, knowledgeable and discreet, and they presented their prime concern as public service in the works rather than private gain. Digges and Borough established themselves as particularly valued and expert advisors, and were regularly commanded to visit Dover in order to view the site and provide authoritative reports to the Lords. Their credentials as practitioners helped to identify them as experts whose judgement could be relied on by the absent Council.88
But social conventions governed more than just the allocation of trust and credit. The proper character of design was also under negotiation. At Dover, the practitioners advocated and practised design as an activity distinct from construction and supervision. The boundary between these domains was an achievement rather than a naturally given distinction. The practitioners established design as a separate terrain and themselves as its proper and most skilful residents. As Digges put it while arguing that the pent walls should be built using the techniques traditionally employed at Romney Marsh:
surely for the long wall these marshmen of Romney are the only and fittest workmen, being guided for the form and some such other points as their skill and experience reacheth not unto.89
Digges implies that he, and mathematical practitioners like him, were to offer the [page 269:] expert guidance required, and thereby make construction dependent on their intervention and design skills.
4. PRACTITIONERS, ARITHMETIC AND MONEY
From the preceding section, it is clear that plats were linked with practical geometry. What of that other pillar of mathematical practice, arithmetic, ‘the ground of arts’? Arithmetic was equally implicated in the design process at Dover.
During the summer of 1579, the Privy Council made explicit the criteria against which designs would be assessed.90 The rules of the game were not complex. It was firstly essential that precious funds should not be wasted on a vain and unfeasible proposal, or one which did not provide a long-term solution. The spectre of Henry VIII’s works looms large in the background to this criterion of technological adequacy and future maintenance.
But technical rationale was not the only, or even necessarily the prime, concern of the Council. Money was of the essence: the project must cost no more than absolutely necessary. If the estimated cost was too great, the project would quite simply receive no central funding. (Not for nothing does the Elizabethan regime have a reputation as notoriously parsimonious.) Moreover, the Council were not to be duped by cunning financial strategies. Construction would begin only on the basis of a sound estimate; money would not later be forthcoming to complete a plan accepted on the basis of an optimistically (or duplicitously) low budget. The Lords indeed had [page 270:] reason to be concerned on this point. In May 1582, Fernando Poyntz was accusing his opponents of just such a strategy. When he had privately voiced his concerns that costs would outstrip the estimates,
Answer was made, tush tush, the plat and estimate must be said to be of small charges to bring [the Council] in and when they be once well entered they must and will proceed to furnish the works as it shall fall out.91
Money and its reckoning were therefore central to the design process for Dover, and we need to examine the practitioners’ financial arithmetic. However, we should not be in too much of a hurry to abandon practical geometry for the undoubted attractions of money: a moment’s reflection reveals arithmetic as an essential prerequisite not only of finance but also of plats and practical geometry.
Within the Euclidean tradition arithmetic and geometry go together. Although often thought of as a purely geometrical text, Euclid’s Elements also contains a theory of numbers (Books VII-IX). Yet the two topics are not established on an equal basis: geometry and geometric magnitude are presented as foundational while arithmetic and discrete number stand as subsidiary and derivative. However, because it requires measurement and calculation, practical geometry presents a different relationship between the two arts. Dealing with numerical dimensions rather than abstract magnitude, practical geometry gives effective parity to arithmetic and geometry. Both arts are resources to be pragmatically drawn on, and textbooks always give extensive numerical examples. Perhaps paradoxically, practical geometry is as much an arithmetical as a geometrical discipline.
The mathematical practitioners therefore had invariably mastered the basic [page 271:] skills of arithmetic. This was more than could be said for a large proportion of their contemporaries. Formal competence in arithmetic was not a necessary accomplishment for many Elizabethans.92 However, arithmetical ability was more widely distributed than were the skills of practical geometry. Merchants, master craftsmen and administrators all required some facility with numbers simply to manage their daily business. The practitioners could not therefore plausibly claim arithmetic as their especial province in the way that they might with practical geometry. Rather than occupying a separate niche, practitioners differentiated themselves at the upper end of a spectrum of attainment, in the avant garde of those advocating the use of arabic numerals and pen reckoning rather than the more traditional Roman numerals and counting boards. Arithmetic was thus less central to the identity of the mathematical practitioners and so I here offer an arithmetical interlude rather than the fuller study that was appropriate for plats.
Aside from the realm of technical feasibility and practical geometry, the Privy Council’s ‘rules of the game’ indicated that financial planning was the primary arena for arithmetic during the design process. A number of examples suggest the extent to which arithmetical ability constrained the work of financial planning.
One of the later design participants was Sir Richard Grenville, who began to interest himself in Dover harbour during 1584. A distant relation of Thomas Digges, he weighed in on the controversial question of deciding the location of the permanent harbour mouth.93 Grenville also set himself up as an amateur expert on [page 272:] stonework and advocated his own jetty design. To support his scheme he provided Francis Walsingham with a scale diagram showing a section of stone wall, and also with technical criticisms of alternative proposals for walls incorporating both stone and chalk. But he also saw the need for a financial justification, in which the unit cost of his scheme could be favourably compared with the current alternative. However, Grenville did not perform the necessary calculations himself: he delegated them to a certain Arthur Gregory who would ‘soon compare and computate’ the relevant costs.94 Grenville evaded the labour of arithmetic on at least one other occasion in connection with Dover, (disingenuously?) pleading lack of time. Yet ability as well as time was clearly involved, for Grenville did not imagine that just anybody could carry out the necessary calculations: he specifically recommended the problem to the attention of either Arthur Gregory (again) or ‘Mr Hill’.95
Grenville’s arithmetical tasks would have required multiplication and division and we may reasonably infer that such operations were at the limits of his competence. The difficulties experienced in carrying out basic arithmetic can also be inferred from the frequency of errors in financial documents. For example, the first proposal prepared by Flemish ‘strangers’ in 1579 contains 5 simple arithmetical errors in a 2½ page document of financial and materials estimates. The cumulative effect of these errors favoured their proposal to the not inconsiderable tune of £438.96 Problems of this kind are even encountered in the documents of mathematical practitioners. In Digges’ ‘Discourse’ to the Queen, there is at least one simple slip and another point [page 273:] at which the arithmetical logic of a calculation becomes tenuous.97 Likewise, problems can be found in Thomas Bedwell’s estimates, and no doubt errors can be found in many other proposals.98 It is of course part of mathematical folklore that mathematicians are often surprisingly slipshod when it comes to simple matters of arithmetic. But my point here is not just the existence of errors; rather, it is that such errors generally went both uncommented and uncorrected. The burden of rechecking another’s calculations seems to have prevented the arithmetical criticism and correction of proposals from becoming a major preoccupation of any of the design participants.
Arithmetical ability (or inability) could thus act as a constraint in financial planning. But it would be quite wrong to see numerical competence solely as a potential brake on the development and assessment of proposals. We also need to consider how arithmetic was creatively used, in particular by the mathematical practitioners.
Some of the most characteristic products of harbour design at Dover were the documents providing costings and estimates for specific proposals. The practitioners provided the most elaborate of these documents, especially Digges who multiplied schemes and sub-options in order to present a full range of costed possibilities; indeed, not only does his ‘Discourse’ present several distinct options but it also refers to further recent proposals which are not given in detail.99 Borough, with his experience of naval accounts and estimates, was also at home amongst such [page 274:] costings.100 The practitioners realised that such documents were essential if the interests of the Privy Council were to be advantageously engaged.
The practitioners’ facility with arithmetic enabled them to transfer and compare notional costs, without remaining rooted only in their own schemes. For example, in the spring of 1582, and again in 1583, Thomas Bedwell prepared a series of papers outlining technical options and associated costs.101 Although he presented and costed his own proposals he was careful to state that his calculations could be ‘applied to any plot exhibited’. Bedwell’s technique was to work out unit costs for different forms of wall and jetty (stone, timber, bavin, and coffer dams of ooze and chalk). He also established prices for single features such as sluices and the cost of operations such as clearing specific areas of the harbour site. He was then able to transfer such abstracted expenditures from one plat to another since, if they were provided with a scale, their relevant dimensions could be measured off. The generation of options and costings then became almost a combinatorial act through which walls, structures, provisions, operations and even people could be swapped, consolidated, tabulated and financially compared.
Aside from establishing unit and overall costs for his own and others’ proposals, Bedwell also worked out an analysis of cash flow, determining the sums of money required per year over the course of the project. Such generalised techniques were aimed at providing the Council with novel insights into likely longer term costs. Bedwell was putting his mathematical skills to work, attempting to make himself useful, irrespective of the perceived merits of his own harbour proposals. His [page 275:] flexible approach meant that even if his own plat was not accepted he might still expect to play a role in the future development of the works.
The practitioners’ financial documents thus did not stand alone. The Council had demanded that proposals be rigorously costed. The practitioners’ response was to tightly integrate costs with the network of people and artefacts which comprised the design process. Their proposals were bolstered by the linkage of money, measurements and scaled plats, to create options which mobilised both technical and financial rationale. Fixed on paper through both practical geometry and arithmetic, the heterogeneous elements of finance, materials and harbour site could be persuasively combined and displayed for the authoritative judgement of the Council.
5. CONTROVERSY, ARGUMENT AND ERROR
On the 15th of August 1580, the Privy Council wrote to the commissioners for Dover harbour that
their Lordships having of late perused two several plots drawn for the repairing of Dover haven, the one by William Borough with the advice of some skilful persons of Dunkirk, the other by one Trew, ... [find] that the first doth require a far greater charge than can be yielded, and that the invention of Trew, tending only to the building up of the pier unto the molehead, doth, in their Lordships’ opinion, carry great likelihood that thereby the haven shall be sufficiently made serviceable with a small charge.102
With this letter the Council set in train the first substantial expenditure on the harbour. However, less than a year later, the Council were again writing to the commissioners [page 276:] with a rather different judgement of Trew:
the plot set down by Trew is not likely to take that good effect we looked for and ... it is now meant that Trew shall be discharged from any further meddling or proceeding in the said works.103
In this final section I want to investigate how, before he had even begun the major business of construction, Trew’s plans were overturned and he was dismissed. Whereas the previous two sections have been primarily analytic, drawing examples from different phases of the design process, this case study discusses a single episode in the development of the project. It shows how mathematical practitioners wove together the resources of history, experience and nature, combining them with plats and money in order to create arguments that could sway the Privy Council.
The principal protagonists in this particular confrontation between competing design proposals were John Trew and William Borough, and Borough is our major source for the conflict. But others do come into the story. Looking back in June 1584 on his participation at Dover, Thomas Digges claimed that he was ‘the first that discovered the gross errors of one Trew’.104 However, his claim is not incompatible with Borough’s primary role: discovery more likely means that Digges was the first to publicly advertise (though not necessarily the first to understand) Trew’s ‘errors’.
When Trew offered his proposal in the summer of 1580, the design process had stalled over the issue of cost. There had already been two plans: Borough’s revision of the original 1576 scheme and the Flemish proposal of 1579. Although differing in details of layout and materials, these two existing submissions had agreed [page 277:] on the principle of a pent. Attention had therefore subsequently shifted to money rather than design and construction. Trew signalled a radically different approach by cutting out the large and expensive pent and concentrating on rebuilding the mole begun by Henry VIII. Costs would be kept low because foundations already existed for his proposed stone wall. Trew reasoned that by building a long wall out into deep water, any shingle brought by the tidal stream of the English Channel would be carried beyond the end of the pier and borne further along the coast to be deposited elsewhere.105 The Council hoped that Trew’s fundamental reappraisal of the design options would result in a harbour costing perhaps one third of previous estimates.106
Who was this John Trew and how did he secure the support of the Council? Trew’s personal status and background are obscure. Apparently from Caerleon in Wales, he was a socially ambiguous figure: although sometimes referred to as a gentleman, his name was only occasionally prefixed by the usual ‘Mr’.107 If his social position is uncertain, his working identity is fortunately clearer. Trew was a projector and inventor, proclaiming skills that clustered around mining and mineral prospecting, the raising and draining of water, provision of labour-saving machines and the construction of fearful engines of war (`I may do as much service at a time of extremity as 5 thousand men, for I can teach to make an instrument that one man shall bear and use without powder that shall do as good service as 3 or 4 [page 278:] calivers’).108 There were many proponents of such marvellous devices but, unlike most, Trew could cite achievements rather than merely extravagant claims. Most importantly with respect to Dover, he had been responsible during the 1560s for an innovative pound lock canal linking the city of Exeter to the sea.109 Trew therefore appeared before the Council as ‘a man well known unto some of their honours to be very skilful in waterworks’.110 His successful persuasion of the Lords rested on the combination of low cost and the technical feasibility warranted by his age and experience.111
Although the Council had favoured his proposal, it did not immediately entrust Trew with the execution of the complete work. The Lords first requested Trew to construct only a short section of his stone wall so that a more reliable estimate of total cost could be established. The negotiations over this trial piece reveal Trew’s characteristic concerns and strategies.
The Council had asked that the test piece should be two rods (33 feet) in length.112 Trew countered by requesting the right to carry out the complete wall and to remain employed until it was finished.113 Evidently unable to dislodge the Council’s self-conscious prudence, he next argued that a trial piece 100 feet long [page 279:] would provide the basis for a better estimate and he reiterated his request to be kept in employment until the end of the project, ‘in consideration whereof he will presently manifest the mystery and skill that he hath given to him’.114 Trew was bargaining the full details of his techniques against a guaranteed position during construction.
There is no sign that Trew won any concessions from the Council and, as a result, it seems that he did not disclose his detailed procedures. In November 1580, when stonework was already in preparation, the commissioners at Dover were apprehensive: ‘by the continuance of the works this year there may be such skill obtained by others that, if it should happen Trew to die, others would be able to finish the same’.115 Trew’s personal presence was essential since his intentions were evidently being communicated only during the course of preparation and construction.
Whereas the mathematical practitioners worked within a paper realm of plats, financial proposals and discursive argument, Trew rested his credentials and credit on his ‘mystery and skill’. There are no surviving plats or documents by Trew: his proposal is known only through administrative documents and the rebuttals of his adversaries.116 Rather than entering into an argumentative exchange of documents, [page 280:] Trew ensured that his knowledge remained personal and private rather than publicly revealed; indeed, he considered his skills to be ‘rare gifts’ which, together with his experience, had been directly given by God.117 Thus when Borough and Digges challenged Trew’s proposal they were doing more than opposing a specific scheme, they were confronting a quite distinct tradition of practice, and a different set of values.
How did Borough and Digges mount their challenge? No doubt they pressed their case through personal contact and discussion; not surprisingly, evidence for such manoeuvres does not survive. But equally, and characteristically, they mobilised resources by producing paper documents and plats. Borough’s substantial contribution is perhaps the most interesting, for it provides a purely presumptive argument. Borough attempted to demonstrate that, even if Trew could successfully construct his scheme, it would inevitably fail in its purpose of securing a reliable and lasting harbour.118 Digges would later offer a similar case, though bolstered by additional criticisms of Trew’s stonework and financial estimates, and of the integrity of the mole’s foundations.119 In seeking to understand how Trew’s position was undermined, I therefore focus on Borough’s efforts, while using Digges as a supplement and confirmation of the practitioners’ tactics.
Borough’s memorandum is rhetorically intriguing. Its fundamental purpose [page 281:] is to cast doubt on the credibility of Trew’s scheme, yet Trew’s name first appears only on the penultimate of the document’s eight pages. Before considering Trew, Borough constructs an historical account of the problems faced at Dover, along with a comparative analysis of relevant harbours elsewhere on the coast. He also provides a resumé of the recent design proposals for Dover, using this narrative to open up the prospect of a revised (and cheaper) version of his own plan. Borough eschews any personally motivated attack on Trew; his discourse studiedly concentrates not on reputation or credit but on ‘mere’ matters of fact. After establishing his seemingly neutral sequence of natural and historical facts, Borough infers the impossibility of Trew’s plans, as if this conclusion was little more than an afterthought.
Consider first the historical argument. By constructing a stone wall on the foundation of Henry VIII’s mole, Trew was effectively consolidating and completing the earlier project. Yet it was common knowledge that this earlier effort had ultimately failed. What was to blame for this previous failure? While it was generally accepted that the beach which blocked the Henrician works had been carried by tidal action along the coast, it was not so clear why it had been deposited within the harbour at Dover. In his 1586 narrative, Reginald Scot reported the stories that he had heard, probably in the town itself. According to Scot, the town had lacked the resources for proper maintenance and the beach entered the harbour through the pier itself, as it began to decay. Once begun, the process was hastened by deliberate destruction and theft, as the poorer townsmen removed valuable timber and ironwork.120
In contrast to this social explanation of failure, Borough and Digges sought [page 282:] to substitute a natural explanation. By shifting the blame from society to nature the mathematical practitioners tried to portray the obstacles as inevitable and the processes as inexorable. Whereas Scot reported the view that poor maintenance had resulted in the harbour’s failure, both Borough and Digges turned this interpretation on its head. They argued that only after witnessing the failure of the harbour did the townsmen despair and allow the pier to decay.121 This historical argument was of crucial contemporary importance. If the Henrician works had miscarried because of natural causes then Trew’s proposal, using the same foundations, would be equally endangered. But to make the historical argument stick, and thus to compromise Trew’s credibility, the motion of the water-borne beach and shingle had to be convincingly demonstrated.
Towards this end, Borough prepared an elaborate comparative analysis which, in abbreviated form, was also used by Digges. Although never referring his endeavour to the canons of natural philosophy, Borough was nevertheless attempting to ground the particular occurrences at Dover in a general pattern of natural behaviour.122 Borough argued that ‘by due consideration of all the havens that I know (such as come out through beach or [are] any ways annoyed therewithal), both in this realm and elsewhere’, the motion of beach is always in the direction in which ‘the flood setteth in every place’. He next contends that beach will be carried along the coast under this tidal impulse until it meets one of two obstacles. If it encounters a ‘ragged point’ such as a jetty or groin it will accumulate until a passage is smoothed, after which time fresh material brought by the tide will be carried further along the [page 283:] coast. Alternatively, if the beach meets with a ‘sharp indraught’ such as a harbour mouth it cannot continue in its path and is deposited, thereby progressively shifting the harbour mouth in the direction of the current’s course.
To buttress this general claim, Borough offered a detailed discussion of Winchelsea and the Camber at Rye, the two harbours that he had previously surveyed as a member of the 1576 commission. Concerning Winchelsea, he asserted that the ‘sharp indraught’ of its harbour had caused beach to accumulate, with the result that the harbour mouth has been progressively shifted eastwards in the direction of the tidal flood. Moreover, since Henry VIII’s reign ‘it is probable that ... there is as much beach increased [there] as is now lying within Dover haven’. Dover’s problems were therefore in principle not unique, but grounded in the common workings of water, tide and beach.
Rye and the Camber prompted Borough to a much longer and more technically demanding discussion. As before, his argument was based on the direction of the tides (whose complex behaviour at Rye he distinguished from that at Dover) and the resultant movement of the beach. He described in detail how the configuration of the coast, the supply of river water and the behaviour and timing of flood and ebb tides had at one time combined to keep the harbour there clear and deep. But whereas Borough could himself remember seeing 52 ships riding afloat there at low water in 1558, the beach was now dry at low water. This alteration he attributed to the inning of inland marshes and to the occurrence of a breach in the waterfront. These events had caused a catastrophic disruption to the local patterns of tide and fresh water flow, resulting in the rapid accumulation of beach and the destruction of the harbour. [page 284:]
Borough’s argument was self-consciously elaborate, drawing on his navigator’s familiarity with tides as well as his knowledge of local topography. From his examples, he concluded that if the pier at Dover was built out to the molehead (as proposed by Trew), the beach would be carried round and into the harbour. There, it would bank up, accumulating to fill the harbour and blocking the mouth. However, lest the complexity of his argument should overshadow the essential point, Borough resorted to the typical resources of the mathematical practitioner:
For explaining of the former discourse, which may seem to be intricate and obscure, the best way is by ocular demonstration, by the view of those plats that I have made for that purpose.
Thus Borough prepared not just local plats such as Figure 5.7 (above, p. 252) but also larger scale ‘demonstrations’ (Figure 5.14), containing detailed notes of tides and a careful delineation of Romney Marsh and the rivers supplying the Camber at Rye.123
With these visual and verbal demonstrations, Borough completed both the historical and natural components of his argument. The deposition of beach was to be understood as an unavoidable outcome of the course of nature. Only the artificial remedy of a pent could be relied on to scour out the harbour and keep it clear, and Borough was thus led back to a discussion and recommendation of his own proposal.
The arguments provided by Borough and Digges were deemed sufficiently forceful by the Privy Council to call Trew’s proceedings into question. Over the summer of 1581, fresh consultations were called and, with the added advice of experts [page 285: Figure 5.14] [page 286:] from the Low Countries, Trew’s proposal was rejected and Trew himself dismissed.
The decisive intervention of Borough and Digges marks this episode as crucial to the development of the Dover project. The techniques that they had used to combat Trew became the de facto standards for the remainder of the works. Through plats, financial estimates and written arguments, design options were to be placed in open and explicit competition. Private knowledge and long experience were devalued, while a new premium was placed on skills in the generation and manipulation of visual, verbal and numerical information. The mathematical practitioners were able to take advantage of the opportunities opened up by this revaluation of design skills. By distinguishing design from construction they entered into the decision-making process as advisors and consultants, while leaving the detailed implementation and supervision to others. Many of their techniques and devices were not in themselves novel: plats and even instruments had been employed in England 40 years earlier. But the practitioners integrated and developed resources that had previously been used only sporadically or in isolation. Once brought together systematically and linked to the programme of the mathematical arts, these techniques established design as principally a paper exercise. With their emphasis on geometry, arithmetic and the culture of measurement, the mathematical practitioners presented themselves as uniquely privileged to occupy this new territory of design.
FOOTNOTES
1. Within the limited space of this chapter I cannot fully consider Dover harbour’s rhetorical and political construction. Among the many documents arguing for the necessity of harbour investment, the most elaborate is by Thomas Digges: ‘A brief discourse declaring how honourable and profitable to your most excellent majesty, and how necessary and commodious for your realm, the making of Dover Haven shall be, and in what sort, with least charge in greatest perfection, the same may be accomplished’, printed in Archaeologia, 11 (1794), 212-254.
2. Digges (footnote 1), p. 239.
3. The reconstruction of harbour design thus has some features in common with Mathew Baker’s transformation of ship design. See chapter 3.
4. A note on sources. My account of the Elizabethan works is based on the primary material of surviving papers and plans, principally those in the Public Record Office (State Papers and Exchequer accounts), the British Library (Lansdowne, Cottonian and Additional collections) and Hatfield House (Cecil Papers, Maps [CPM]). Although not free from errors and misinterpretation, much the best modern account of the works is by John Summerson in H.M. Colvin (ed.), History of the King’s Works, 6 volumes (London, 1963-82), IV, 755-764. Although aware of some important documents apparently unseen by Summerson, the discussion of the Elizabethan works in Alec Hasenson, The History of Dover Harbour (London, 1980) is unreliable. L.E. Harris, The Two Netherlanders. Humphrey Bradley and Cornelis Drebbel (Leiden, 1961), chh. 1 and 2 provides a sketch of Dover primarily as a background to Bradley’s later career. Moreover, though they usefully reproduce and discuss some of the surviving plats, the attributions and interpretations of two earlier papers are not always trustworthy: William Minet, ‘Some unpublished plans of Dover harbour’, Archaeologia, 72 (second series, 22) (1922), 185-224 and Alec Macdonald, ‘Plans of Dover harbour in the sixteenth century’, Archaeologia Cantiana, 49 (1938), 108-126. I have also used the retrospective narratives of two participants: ‘The note of Reginald Scot esquire concerning Dover haven’, written in 1586 and published in Holinshed’s Chronicles, 6 volumes (1807-8 ed., facsimile New York, 1965), IV, 845-868 and John Tooke’s 1604 manuscript ‘Discourse of Dover Harbour’ (BL Add. MS 12514, ff. 33r-45v). When basing themselves on their own first hand experience, Scot and Tooke give many valuable details (even extending in Tooke’s case to reported speech). But their narratives cannot be accepted uncritically. When describing events prior to their own involvement, their accounts need to be corrected against other material: despite Summerson’s assurance to the contrary (p.755), Scot’s narrative does indeed conflict with the documents, crucially so on at least one point. Tooke, too, was not always well-informed and occasionally garbled chronology and other details.
5. For the Henrician works, see Martin Biddle’s account in Colvin (footnote 4), IV, 729-755.
6. Scot (footnote 4), p. 848.
7. For Dover petitions and ambassadorial complaints, Summerson (footnote 4), p. 755.
8. The device for the Rye, Winchelsea and Dover bill is SP12/107/47. For the 1576 parliamentary committee, Commons Journals I, p. 105b. The briefing document for the investigating commission is Lansd. 22/10, f.36r.
9. The sluice-controlled pent at ‘Newhaven’ (Le Havre) was well-known to English experts, while there were also examples to be found in contemporary developments in the Netherlands. On Le Havre, William Barclay Parsons, Engineers and Engineering in the Renaissance (Cambridge, Mass., 1939/1968), ch. 28. For Dutch practice, J.P. Sigmond, Nederlandse zeehavens tussen 1500 en 1800 (Amsterdam, 1989) and, for a briefer account, idem, ‘Development of Dutch harbours 1500-1800: a survey’ in Simonetta Cavaciocchi (ed.), I Porti come Impresa Economica (Prato, 1988), 881-907.
10. For the details of this and succeeding paragraphs, Summerson (footnote 4).
11. G.R Elton, The Parliament of England 1559-1581 (Cambridge, 1986), p. 258. The unique character of such national funding for an Elizabethan harbour is emphasised by J. Summerson, ‘The defence of the realm under Elizabeth I’, in Colvin (footnote 4), IV, 402-14, p. 408.
12. The interpretation of Trew and the events of 1581 is the weakest part of Summerson’s account (footnote 4). I discuss these matters more fully in section 5 below.
13. Scot (footnote 4) deliberately omitted discussion of the harbour mouth controversy but, as a proud participant, Tooke (footnote 4) reproduced many details of the events.
14. Scot (footnote 4), p. 845.
15. Commons Journals, I, p. 105b.
16. Lansd. 31/74 and 40/79 (copy at SP12/171/13.i).
17. SP12/153/8, SP12/153/15.i and SP12/160/13.i.
18. Lansd. 22/10, f. 36r-37r (a copy, made five years later by Borough, of the original 1576 commission and the commissioners’ response).
19. SP12/131/72, /72.i, SP12/153/15, SP12/153/64, SP12/158/46, SP12/158/72, SP12/160/3.
20. Lansd. 22/10.
21. SP12/45, f. 19v, SP12/159/11, SP12/160/6.
22. For Digges on the form of the walls, see his initial proposals to the Queen (footnote 1), p. 236 and his 1583 views in Lansd. 40/85 and SP12/159/26. Borough’s 1583 wooden wall proposal is SP12/160/3.
23. For the harbour mouth controversy, see Tooke (footnote 4) and, for Digges’s arguments, Lansd. 40/79, 40/84, 40/80.
24. For Borough as a signatory to the 1593-4 accounts, see PRO E101/543/16.
25. Lansd. 22/10, f. 36r-37r.
26. SP12/160/3.
27. SP12/161/4.
28. SP12/153/27, /28.
29. SP12/153/61.
30. SP12/155/14, SP12/156/14, SP12/156/23, /24, SP12/158/78.
31. Bedwell’s last Dover intervention seems to be a document of 7 March 1582/3 presenting his views on the pent walls (SP12/159/9).
32. SP12/161/7.
33. SP12/164/12, /13, /17, /25.
34. SP12/173/27, /27.i.
35. SP12/171/49.
36. SP12/172/13, SP12/173/18.
37. Despite Summerson’s claim (footnote 4, p. 762) that Ive would have been occupied at Dover for most of 1585, he had already been discharged by the end of 1584: SP12/175/40.
38. For examples of the many surviving letters from Hill to Walsingham, see SP12/173/11, /18, /27, /46, /68, /77, /93 from September and October 1584.
39. For Hill as auditor, see PRO E101/543/13-16.
40. On Poyntz, see Harris (footnote 4), pp. 17-19.
41. Stonham was irregularly but sometimes intensively employed at Dover between at least 1579 (PRO E101/543/4) and 1595 (PRO E101/543/17). On Stonham, see Graham Mayhew, Tudor Rye (Falmer, 1987).
42. For Flemish and other Low Countries workers: SP12/131/72.ii, SP12/120/24, SP12/152/78 (1579), SP12/45, f. 19v, SP12/150/82 (1581), SP12/172/10, /11 (1584). Humfrey Bradley, responsible for a long report of 1584 ((SP12/173/96) also came from the Low Countries; see Harris (footnote 4).
43. No reliable estimate of the total number of later 16th century Dover plats is possible. Apart from the vagaries of survival, there is a troublesome problem of language: just like the modern usage of ‘plan’, plat was used in the 16th century to refer both to drawings and also to written proposals. (Indeed, it should not be forgotten that the word had a whole range of even richer connotations and associations; see Oxford English Dictionary). It is thus often difficult to tell whether a participant’s reference to a plat should be taken to mean a text or a picture. For the sake of clarity in the present discussion, I restrict the use of ‘plat’ to drawings alone. However, I do not mean to suppress the importance of the written proposals: the significant links between verbal plans and visual plats will be discussed below.
44. Plats were first integrated with the mechanisms of English government under the direction of Henry VIII. The Dover plats of the 1530s were part of this larger development; Peter Barber, ‘Henry VIII and mapmaking’, in David Starkey (ed.), Henry VIII. A European Court in England (London, 1991), 145-151 and, for a fuller treatment, ‘Pageantry, defense, and government: maps at court to 1550’, in David Buisseret (ed.), Monarchs, Ministers and Maps: the Emergence of Cartography as a Tool of Government in Early Modern Europe (Chicago, 1992), ch. 2. Cartography was already being integrated within the state’s operations in 15th-century Venice; Denis Cosgrove, ‘Mapping new worlds: culture and cartography in sixteenth-century Venice’, Imago Mundi, 44 (1992), 65-89, p. 69.
45. Lansd. 22/10, f.36r.
46. Biddle (footnote 5), p. 732 and Barber, ‘Henry VIII and mapmaking’ (footnote 44), p. 147. For more on Volpe, see Roy Strong, The English Renaissance Miniature, revised edition (London, 1984), p. 29.
47. Tooke (footnote 4). The plat is BL Cott.Aug.I,ii,9.
48. From within the history of cartography, J.B. Harley has also criticised the notion of measurement as objectivity; see his ‘Silences and secrecy: the hidden agenda of cartography in early modern Europe’, Imago Mundi, 40 (1988), 57-76, which gives further references.
49. PRO MPF 141.
50. Sir Thomas Scott to Francis Walsingham, 21 July 1583; SP12/161/39. Both the specificity of the numbers and the description of the survey as a ‘perfect measure’ suggest that the (unnamed) surveyor provided much more than just a rough and ready estimate. The results for the areas were: great pent, 17½ acres; lesser Paradise pent, 4 acres (minus 15 perches); and the harbour area itself, 15 acres.
51. Digges (footnote 1), p. 221.
52. SP12/164/13, /12, /17, /25. Further sounding work was being discussed in 1584: SP12/172/10 and /13.
53. Sir Thomas Scott to Henry Guildford, 8 November 1583; SP12/163/58 and /58.i.
54. SP12/164/25.
55. SP12/172/13.
56. For the multiple purposes of Elizabethan maps and plats, see P.D.A. Harvey, Maps in Tudor England (London, 1993), pp. 23-5.
57. Previous studies have been unable to adequately establish the authorship, purpose and context of this plat. The interpretations of Minet and MacDonald (footnote 4) and R.A. Skelton and John Summerson, A Description of Maps and Architectural Drawings in the Collection made by William Cecil First Baron Burghley now at Hatfield House (Oxford, 1971) all contain more or less obvious flaws. As with several other Dover plats, a full examination of authorship and purpose would require a substantial discussion. Fortunately, the present discussion does not depend on a conclusively established attribution.
58. For this widespread form of plat, see Harvey (footnote 56), p. 17. The absence of a scale on this particular plat might only be apparent, for the plat may have been cropped at the bottom. In terms of pictorial composition, the lower detail is compressed and given no adequate border; indeed, the ‘Moule’ is almost cut off by the edge. A (now lost) lower section would have been a likely location for a linear scale, as witness the Digges plat (Figure 5.2).
59. Note that the observer firstly had to adjust the landmark’s tabulated height since the observation was unlikely to be made at exactly high water mark (itself not a precisely defined reference level). This procedure for determining distance is merely the inverse of one spelled out in contemporary texts. For example, in Leonard Digges’s Pantometria (1571), I, 30, it is shown how to instrumentally determine the distance of a ship at sea when observed from the shore. That the table of Figure 5.7 is not for Digges’s purpose but for its inverse is clear from the nature of the landmarks cited. Positions such as the top of a chimney are not places on which one could stand and take instrumental measurements, they are marks to aim at.
60. The same result can be achieved without the need for a compass bearing if two rather than one of the landmarks are observed. The practitioner’s position can then be triangulated on a plat.
61. There are some suggestive contemporary comments on the importance of appearance. For instance, in 1582 Fernando Poyntz complained when a new plat prepared by Digges, Borough and the commissioners was presented: ‘it is said my simple plat is overcome by silver shows, but golden senses are to esteem the value of them both’ (SP12/159/18.i; copy at Lansd. 34/61). Earlier, in August 1579, the commissioners had sent Borough up to the Council from Dover with a plat ‘very handsomely set out’ (SP12/131/72).
62. As with my discussion of ship design on paper (chapter 3), I have drawn here and below on Bruno Latour, ‘Visualization and cognition: thinking with eyes and hands’, Knowledge and Society: Studies in the Sociology of Culture Past and Present, 6 (1986), 1-40.
63. See, for example, SP12/152/33 and /87, Digges (footnote 1) and SP12/153/51.
64. This significant plat does not appear to have previously entered the literature. As with 7, it is unfortunately neither signed nor dated and a full presentation of the evidence for authorship and context would take many pages. Fortunately for present purposes, the precise details of my attribution to Bedwell are again not essential; rather, we need to establish only that it is the product of mathematical practice. Note in particular that it offers a purely plan view, stripping away topographic details of town and castle; that it provides a scale; that the lengths of the pent walls are given; and that it displays a computation of the harbour areas created under its different options.
65. I would like to record my thanks to the Conservation Department of the Public Record Office (Chancery Lane) who kindly removed small pasteovers and reattached them as flaps. Their work has permitted me to make an almost archaeological investigation of an artefact that would normally be classed as only two dimensional. On the lower of the two options for a pent, there is a third pasteover covering the sluice or gate at the top end of the diagonal cross wall. Unfortunately, its removal would have endangered the integrity of the plat as a whole; it therefore remains firmly attached.
66. 27 June 1582; SP12/154/20.
67. SP12/159/11.i, with copy as /11.ii.
68. SP12/159/8.i, copy at Lansd. 34/61.
69. By presenting the issue in these terms I want to avoid attributing power to plats as if it was somehow an inherent property rather than a consequence of their use, cf. Bruno Latour, ‘The powers of association’, in John Law (ed.), Power, Action and Belief. A New Sociology of Knowledge?, Sociological Review Monograph, 32 (London, 1986), 264-280.
70. Lansd. 22/11.
71. Borough, for example, frequently used plats in conjunction with speech: Lansd. 22/10, f.36v (1576), SP12/131/72 (1579), and SP12/153/64 (1582).
72. Digges (footnote 1), pp. 227, 228 (twice), 229 and 231; also Lansd. 40/80, endorsed 24 June 1584 (with another unsigned copy at SP12/171/13.iv).
73. Borough forcefully used this tactic in 1581: Lansd. 22/10, f. 35v, and see section 5 below. Foreigners or ‘strangers’ such as Humfrey Bradley also interlinked text and ‘card’: SP12/173/96, paras 35 and 41.
74. Lansd. 40/84.
75. For models as diagrams, see SP12/152/59 to /64, a miscellaneous collection of wall and jetty sections and schemes for stonework. Fol. 106v is dated 9 March 1581/2 and titled ‘draughts for stonework at Dover’; a different hand has added ‘Modells’ as an alternative title.
76. For these references to models of structures and mechanisms, Digges (footnote 1), pp. 225, 228, 229, 234, 236.
77. Lansd. 22/11 (anonymous but by Digges?), SP12/153/61 (Thomas Bedwell) and Lansd. 37/67 (Fernando Poyntz).
78. E/101/543/6. When discussing stonework, Digges’s references to models may therefore not be only to paper diagrams; Digges (footnote 1), p. 240 and Lansd. 31/74.
79. For Pett and Baker’s models, Scot (footnote 4), p. 853 and E101/543/8. Borough, who sided with Pett and Baker on the question of wooden walls, submitted a revised harbour scheme on 3 April 1583 with walls to be built ‘according to the model and the minds of Peter Pett and Mathew Baker her Majesty’s Master Shipwrights’ (SP12/160/3). Stonham’s model is of later date, and was paid for in 1591-2. Although the harbour accounts give no indication of its material, the extraordinarily high cost of £7.15.0 suggests that it could not be merely a paper artefact (E101/543/14).
80. Even when the Council decided to visit the works at Dover in 1586, events conspired to frustrate their intentions; Scot (footnote 4), p. 845. Note however that Lord Burghley did himself make the journey in the summer of 1583, specifically ‘to examine the new works of the harbour’ (Cecil Papers, Accounts 4/16; cited by Skelton and Summerson (footnote 57), p. 47).
81. For a larger-scale and more systematic historical case study of remote control and action at a distance, see John Law, ‘On the methods of long-distance control: vessels, navigation and the Portuguese route to India’, in Law (footnote 69), 234-263. Also note Bruno Latour on Lapérouse and action at a distance in Science in Action (Milton Keynes, 1987), chapter 6.
82. Steven Shapin and Simon Schaffer, Leviathan and the Air-Pump (Princeton, 1985), chapter 2.
83. Digges (footnote 1), p. 241.
84. John Hill to Francis Walsingham, 18 September 1584: SP12/173/18.
85. SP12/156/14, /23, /24.
86. For example, SP12/153/56 (May 1582), SP12/156/4 (6 December 1582), and Lansd. 31/66 (5 April 1583).
87. For example, Lansd. 40/79 (copy at SP12/171/13.i).
88. See SP12/45, f.19v and SP12/153/8 for examples of the Council’s reliance on Digges and Borough.
89. Digges to Walsingham, March 1583, SP12/159/26.
90. Privy Council to Lord Cobham, SP12/140/46.
91. SP12/153/56. Of course, Poyntz may have been deliberately playing on the Lords’ fears to win credit for himself.
92. Keith Thomas, ‘Numeracy in early modern England’, Transactions of the Royal Historical Society, 5th series, 37 (1987), 103-132. Thomas’s account provides a useful background to my discussion of arithmetic.
93. The best account of Grenville’s involvement in this episode is given by John Tooke (footnote 4).
94. SP12/173/95 and /95.ii and iii. Gregory was a versatile cryptographer and military engineer who devised a special coach for Burghley, with compartments for papers and a ‘portable counting house’; see Summerson, ‘Defence of the realm’ (footnote 11), pp. 413-4.
95. SP12/172/57.i. Presumably Mr Hill was auditor John Hill, then at Dover.
96. SP12/152/78.
97. Digges (footnote 1), p. 235, where £476 rather than £576 is given as the projected cost of Digges’ southern jetty; and p. 236, where the calculation for the ‘embowed bay’ is even more troublesome.
98. In SP12/153/28 and /29 Bedwell seems to have incorrectly computed the tonnage of beach piled to a depth of 10 feet.
99. For other financial documents prepared by Digges see, for example, SP12/153/51 and Lansd. 40/85.
100. For example, SP12/160/3.
101. The following points are based on SP12/153/28 and /29 (April 1582), SP12/153/61 (21 May 1582), and SP12/159/9 (7 March 1583).
102. Acts of the Privy Council (APC), 12, p. 161. In this first letter Trew is referred to as ‘Drew’. I have substituted the spelling used in all other sources.
103. SP12/45, f. 19v. Although surviving only as an undated copy, this letter must have been written between 14 June 1581 (APC, 13, p. 80) and 26 July (APC, 13, pp. 139-40).
104. Lansd. 40/79; copy at SP12/171/13.i.
105. Borough reports that Trew did propose to construct a (presumably small) pent within the town itself, though evidently thinking that its scouring effect was hardly necessary; Lansd. 22/10, f. 35r. Digges placed Trew’s sluices in the meadows above the town; Lansd. 31/74, f. 187r.
106. SP12/141/27. Borough reported Trew’s offer as £8,000 or £10,000; Lansd. 22/10, f. 35r.
107. For Trew’s Welsh origins and references to him as a gentleman, see the draft commissions empowering him to take up labour and purchase materials; SP12/142/14 and /15. Although Trew must have owned some land to justify the title of gentleman, his petitions to Burghley and the Queen (see footnote 108) indicate that he had no substantial wealth.
108. Lansd. 107/73 and SP12/219/52.
109. For Trew’s Exeter canal, which ultimately involved Trew in lengthy litigation, Philip Chilwell De la Garde, ‘On the antiquity and invention of the lock canal of Exeter’, Archaeologia, 28 (1840), 7-26, idem, ‘Memoir of the canal of Exeter, from 1563 to 1724’, Minutes of the Proceedings of the Institution of Civil Engineers, 4 (1845), 90-102 and W.B. Stephens, ‘The Exeter lighter canal, 1566-1698’, Journal of Transport History, 3 (1957), 1-11. Kenneth R. Clew, The Exeter Canal (Chichester, 1984) adds nothing of substance.
110. Lansd. 22/10, f. 35r.
111. In November 1580 the commissioners commented that Trew was an old man; SP12/144/8. (The printed Calendar of State Papers renders Trew as an able rather than an old man!)
112. SP12/141/27.
113. SP12/142/1.
114. SP12/142/3.
115. SP12/144/8. By December 1580, Trew had 40 ‘hardhewers’ and 60 labourers at Folkestone quarry and had arranged for 100 labourers and workmen to begin preparations at Dover; SP12/144/55.
116. Summerson (footnote 4), p. 757 n.1 tentatively suggests that SP12/141/58, an estimate for a £7000 harbour at Dover, may be by Trew; although lacking conclusive disproof, I do not believe that this attribution can be sustained. It is important to emphasise that, from Reginald Scot’s 1586 account onwards, the absence of papers by Trew has resulted in a universal misinterpretation of his proposal. Scot was a diligent historian: we can often precisely pinpoint the documents that he was using when writing his retrospective narrative. However, although he was able to specify the large sums of money spent by Trew, Scot did not have reliable information on the purpose of this expenditure (footnote 4, p. 851). Scot represented Trew as the advocate of a stone wall running the length of the bank of beach from the town to the harbour mouth, and he has been followed by all subsequent historians. Scot may have seen and misattributed the town’s own plat, drawn up by John Lucas, which depicts just this option of a long stone wall along the bank of beach (see above, p. 247).
117. Lansd. 107/73.
118. ‘Notes touching Dover haven’, Lansd. 22/10, ff. 32r-35v. At ff. 36r-37r, Borough demonstrated his long-standing Dover involvement by providing copies of the original commission of 1576 and the commissioners’ report.
119. Lansd. 31/74, ‘The reasons that moved the Commissioners for Dover Haven to condemn the works begun by John Trew’. Despite its apparently communal title, this is signed only by Digges. On the basis of handwriting and terminology, Lansd. 22/11 (`Notes touching the decay and remedy of Dover haven’) may also be by Digges. While covering many of the same issues, it offers a more exploratory treatment. As its attribution is not conclusively established, I have not included it as part of my account.
120. Scot (footnote 4), p. 849.
121. Lansd. 22/10, f. 32r and Lansd. 31/74, f. 186v.
122. When writing on related topics such as the formation of sandbanks and the erosion of coastlines, William Bourne did choose to dignify his discussion as natural philosophy; see book 5 of the Treasure for Travellers (London, 1578). However, in its content and presentation, Bourne’s text is no closer to contemporary natural philosophical convention than Borough’s.
123. This plat was first attributed to Borough on stylistic grounds by R.A. Skelton, ‘Two English maps of the sixteenth century’, British Museum Quarterly, 21 (1957), p. 1. The attribution was accepted by A.H.W. Robinson who, interpreting it as a partner to a similar plat from 1596, dated it accordingly; Marine Cartography in Britain (London, 1962), p. 31. However, from the form of Dover harbour (always carefully represented by Borough), it is clear that this plat dates from before 1583. Borough’s participation in the Dover project provides the best context for its preparation.