Making the arithmometer count
Introduction
The arithmometer of Charles Xavier Thomas de Colmar (1785-1870) has a firmly established place in the history of computing. While the lion’s share of recent scholarly attention has been lavished on Charles Babbage’s difference and analytical engines, historians examining calculation in the 19th century have nevertheless repeatedly affirmed the importance of Thomas’s device. Typical characterisations are remarkably uniform: ‘the first multiplication machine to be made commercially for general sale’, ‘the first commercially successful calculator’ and ‘the first commercial calculating machine’.1
The arithmometer was not however the first machine to accomplish the four basic arithmetical operations of addition, subtraction, multiplication and division – earlier machines such as those of Hahn and Müller had achieved this level of functionality in the 18th century.2 But the implied virtues of the arithmometer are clear. Lacking the mathematical ambition driving the work of Babbage and his followers, the machine was solid, dependable and successful, an industrial product manufactured in quantity.
Yet despite this apparent consensus there are striking problems with standard accounts of the arithmometer. Rather than a smooth passage to success, I will suggest that the machine’s early decades witnessed a different and more troubled trajectory, in which the mechanical and public character of the arithmometer was repeatedly transformed. This process of development took place over an extraordinarily protracted period. Although first made public in 1820, a lengthy report of 1878 remarked that the arithmometer had still not taken its ‘rightful’ place in industry.3 Perhaps this perception of failure should be attributed to the overoptimistic expectations of a sympathetic advocate. But the widespread acceptance of the arithmometer cannot be dated much before the late 1870s. Only then was the machine deemed sufficiently successful to be worth copying, when arithmometer ‘clones’ were first manufactured in Germany by Burkhardt and, slightly later, in Britain.4
In this paper I focus on the period of more than 50 years between the invention of the machine and its establishment as an accepted instrument of calculation. I examine three aspects of the arithmometer’s early history: its development as a mechanism, the means used to publicly promote it and the concrete ways in which it was adopted by an expanding circle of users. This multiple approach seeks to reveal the technical, promotional and personal investment required before the arithmometer could be ‘counted on’, not just in the straightforward arithmetical sense but also counted on as a reliable resource for a whole range of potential users.
Design and development
Examples of the arithmometer survive in many public and private collections. Yet despite its easily recognisable outward appearance, we should be wary of discussing the arithmometer, as if the machine existed in a single unchanging form. A few of the machine’s basic principles did remain constant but almost every feature of their implementation was altered by Thomas. Moreover, the long list of internal and external changes does not represent simply a uniform sequence of improvement. In some of the most important instances of redesign Thomas did not just rectify or add to an existing model; rather, he attempted to redefine the character and the ambitions of the machine, and thus its possible market.
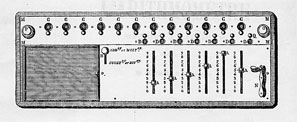
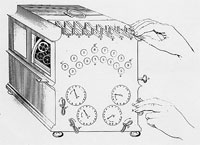
The familiar features of the mature version of the arithmometer provide a convenient standpoint from which to survey its changing form and operation. The machine presents two principal parts, a fixed setting plate with a series of sliders for inputting numbers (fig. 1: A), and a movable carriage where results appear (fig. 1: M). A number set with the sliders is mechanically transferred to the result dials on the carriage (fig. 1: C) by turning the handle (fig. 1: N). This transfer operation, basic to all the arithmometer’s workings, is accomplished using the celebrated stepped cylinders first introduced by Leibniz.
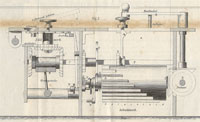
Each cylinder carries 9 teeth whose length increases stepwise (fig. 2: A). The cylinder’s teeth engage a pinion (fig. 2: B) whose position is controlled by the setting slider (fig. 2: C). The higher the number set by the slider, the larger the number of teeth on the cylinder engaging the pinion. When the handle is turned the cylinder rotates and as a result the pinion’s square arbor (fig. 2: F) is turned through an arc proportional to the value set on the slider. It is this rotation which is communicated to the result dial (fig. 2: K) via a bevel wheel (fig. 2: G). One turn of the handle adds the value set on the sliders to the result dials and, since multiplication is simply repeated addition, turning the handle, say, 5 times multiplies the given number by 5. To multiply by 25 it is not necessary to turn the handle 25 times. Rather, after turning it 5 times the carriage is moved one step to the right and the handle then turned two times.
Using the reversing switch on the setting plate (fig. 1: B), the machine can be set to perform subtraction and division. Figure 2 shows the result of pushing the switch: M slides forward, disengaging the bevel wheel G from I (on the axis of the result dial K) and bringing H into contact with I. Now when a turn of the handle causes arbor F to turn, I – and thus the result dial – rotates in the opposite direction, reducing rather than increasing the displayed value. A turn of the handle thus subtracts the number set on the sliders from a number entered on the result dials.
As multiplication is repeated addition, so division is repeated subtraction, with the quotient appearing in the smaller set of dials on the carriage (fig. 1: D). These quotient dials are simply counters: each turn of the handle increments the dial currently in contact with the counting mechanism by one unit. The quotient dials are also useful in multiplication, since they provide a visual check on the value [page 13:] of the multiplier. Finally, when a calculation is complete, the carriage dials can be reset to zero: each set of dials has an independent zeroing mechanism operated by twisting one of the two knurled knobs at either end of the carriage (fig. 1: O and P).
The engraving in figure 1 is from an instruction booklet of 1865. Some measure of the operational transformation of the arithmometer can be gained by turning back to the debut of the machine.
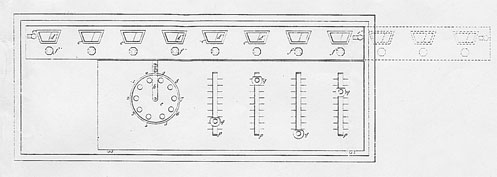
Thomas’s arithmometer was first made public in 1820 when he was granted a five year patent for his calculating machine (fig. 3).5 It is clear however that the patent represents only a transient prototype, on which Thomas was still actively working. By 1821, when he was ready to submit an example to the scrutiny of the Société d’encouragement pour l’industrie nationale, the design had already moved on significantly. The Société’s Bulletin first featured a short report on the arithmometer and then a longer illustrated memoir.6 A machine almost identical to the engraved design of 1821 survives in the Smithsonian’s National Museum of American History (figs 4 and 5).7 The inscription on the setting plate records not only the machine’s inventor but also – apparently uniquely on a surviving Thomas machine – who actually made it, the Parisian mécanicien and clockmaker, Devrine.8
By comparison with figure 1, several features stand out in these early designs. To focus primarily on the Smithsonian machine, it clearly has a smaller capacity: there are only three setting sliders. Alongside these sliders there is a fourth slot identified as the ‘multiplicateur’, which is conspicuously absent from the machine of the 1860s. The multiplicateur was intended to abbreviate multiplication and division. Setting a figure on the multiplicateur and actuating the machine caused the stepped cylinders to rotate the desired number of times. Thus, in multiplying by eight, for example, a single operation was required rather than the repetition of eight actions.9
The carriage contains no quotient dials but only a series of paired result dials. Without a switch on the setting plate to alter these dials’ direction of rotation, subtraction and division are accomplished by an alternative and less direct route. Each result dial carries two concentric sequences of numbers, one increasing for addition the other decreasing for subtraction. In revealing one sequence the other is hidden, so the user had to choose the appropriate number sequence for the desired operation. (Pascal had resorted to similar means in his 17th-century adding machine.) Each of these dials has to be individually reset by twisting the knob mounted on its axis: there is no general zeroing mechanism. Finally, it is perhaps easy to overlook the lack of a handle. Instead there is a silk ribbon which is pulled outwards to set the machine in motion.
Even dwelling only on external features makes clear the substantial gap between the early versions of the arithmometer and those of the 1860s. However, the development path from one to the other was neither straightforward nor steady. After the initial fanfare of favourable reports in the Bulletin of the Société d’encouragement, nothing further seems to have been heard of the arithmometer for more than 20 years. At this stage in its development the machine appears no different from the many earlier arithmetical machines that had been announced, had demonstrated their feasibility through working prototypes and then sunk without further trace.
Later publicity material claimed that Thomas had worked incessantly to develop the machine from 1820 onwards,10 but the apparent absence of any promotional effort for over two decades warrants at least some scepticism over such claims. Nor would it be surprising if the arithmometer had been set aside. Thomas was not a mechanician whose professional success rested on his ability to create and sell a working commercial machine. Rather, he was the director of an insurance company, and was presumably preoccupied with this work for most of his professional life.11
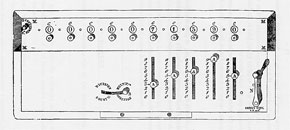
However, the arithmometer did re-emerge. A machine of unknown design was displayed at the 1844 French national exhibition and, by at least 1848, a thorough redesign had been carried out. The ribbon drive was dispensed with and replaced by a crank handle inserted into the front of the box. The capacity was increased to five setting sliders and 10 result dials. The multiplicateur slide was retained from the 1820s machine but must have had a new mechanism, while there was now a wing nut on the setting plate for switching between addition and subtraction, dispensing with the doubly numbered result dials.12
These changes heralded a decade of further development, the most intensive in the arithmometer’s history. A patent for a new and more compact machine was obtained in 1850.13 As well as the reduction in size, the position of the handle was altered and a zeroing mechanism added (fig. 6). But this model was, in turn, quickly superseded by another new machine in 1852 (fig. 7).14 As well as incorporating some relatively cosmetic changes, such as a new form for the add/subtract switch and for the zeroing button, the 1852 machine also marked a more fundamental departure in Thomas’s approach and strategy. While the succession of previous models had incorporated mechanical changes, they had nevertheless retained the same functional elements. The new model of 1852 jettisoned the multiplicateur, making the machine simpler (and therefore presumably [page 14:] cheaper to construct), but in effect less powerful. The user rather than the machine now had to keep count of the turns of the handle, especially when performing division.
Thomas evidently experimented with means to supply this lack,15 but it was not until 1858 that the absence was definitively remedied by the introduction of quotient dials on the carriage.16 By this stage the arithmometer had, outwardly at least, achieved its classic form, though it was not until the mid-1860s that the quotient dials received their own zeroing mechanism.
This sketch of the changing form of the arithmometer has only covered some of its more obvious and external alterations, those which reveal the changing options and operations available to a user. But these do not necessarily represent the machine’s most significant transformations. The development and ultimate abandonment of the multiplicateur required major internal redesign, for example. However, contemporaries agreed that the most challenging task for the devisor of calculating machines lay in the creation of the tens carry mechanism.17 Without delving into the mechanical intricacies, we can note that Thomas redesigned this element more than any other: the arithmometer exhibits at least 5 distinct mechanisms up to the 1860s. These alterations responded to publicly voiced concerns about the delicacy of the tens carry, and sought to guarantee robustness by reducing the reliance on springs as transmitters of force.18
The hidden revisions to the arithmometer’s innards extended beyond the sensitive element of tens carry to such basic features as the drive transmission, which was altered from a gear train to a shaft. Such internal alterations provide probably the best evidence that the performance of the machine was open to improvement. Even that most fundamental mechanical organ of the machine, the stepped cylinder, did not remain unaltered. Although its wording and illustration is obscure, and there is no surviving machine available for clarification, it is clear from the 1820 patent that Thomas’s initial design for the cylinder incorporated an additional tooth, subsequently discarded, which was engaged as part of the tens carry mechanism. Moreover, rather than 9 stepped teeth the Smithsonian example’s cylinders have 18, arranged in pairs.
Although further refinements would continue to be introduced by Thomas’s business successors and their competitors, by the 1860s arithmometers were being produced in a form which remained relatively stable until the First World War. This familiar form of the arithmometer may clothe it in a guise of solidity and permanence. But by surveying the machine’s technical development we can see how shifting and fragile was its identity over a period of 50 years.
Promotion and competition
Focusing on the machine itself provides one strand of development. But how did the arithmometer fare in the public realm? The arithmometer had first become public when it was patented in 1820. This claim expired after 5 years and it was not until 1850 that fresh legal rights were obtained. From this point a more systematic policy was pursued, and the 15 year rights were extended and renewed in 1865 and 1880.
While the patent documents included mechanical description and illustration, such information was also made accessible by other forms of publication. Machines were offered to learned and improving societies with the expectation that they would be reviewed. The reports on the construction and use of the arithmometer for the Société d’encouragement in 1821, 1822, 1851 – when it was awarded a gold medal – and, after Thomas’s death, in 1878 have already been cited. A machine was also presented to the Académie des Sciences in 1854 and a report duly followed later the same year.19
Patent specifications and journal reports thus repeatedly served as a medium for accounts of the arithmometer, typically focusing narrowly on the form and operation of the machine itself. However, the contexts in which the machine was communicated and assessed multiplied from the 1840s. Exhibitions, newspapers, popular scientific periodicals and promotional material on behalf of the machine all offered the arithmometer to a wider audience.
When presented through these media the arithmometer was placed in open competition with other devices. Although now often presented as a lone pioneer,20 the arithmometer jostled with other machines for attention and acclaim. Far from being a self-evident success it was frequently ranked as merely second best in its class. The public career of the arithmometer in the 1840s and ’50s suggests how much work was required to establish the name and reputation of Thomas’s machine.
Thomas first ventured into the world of exhibitions when the arithmometer was revived in 1844. A machine was entered in the French national exhibition of industrial products where it was classed amongst precision instruments in a category of ‘diverse measures, counters and calculating machines’. If Thomas had hoped for substantial recognition and reward, he was to be disappointed. The arithmometer was granted an honourable mention in the jury report but was clearly considered inferior to the submission of the Hungarian emigré doctor Didier Roth, who obtained a bronze medal for his adding and calculating machines and counters. Roth had been actively promoting his adding machines since 1842 and had received a favourable report from the Société d’encouragement in 1843. The judgement of the 1844 jury was mirrored in the coverage given to Roth in a separate guide to the exhibition’s highlights, in which Roth’s adding machine was described and illustrated, while the arithmometer was ignored.21
The next French national exhibition took place in 1849 and Thomas again tried his luck. On this occasion he was awarded a silver medal and the jury report devoted three pages to his machine.22 However, despite this higher honour, he was again eclipsed, for a gold model went to the mechanicians Maurel and Jayet for their ‘arithmaurel’, a calculating machine with automatic capabilities judged to exceed those of the arithmometer. [page 15:]
A further competitive opportunity was soon offered by the 1851 Great Exhibition. But again, Thomas was frustrated. The arithmometer was one of two calculating machines to receive a prize medal, but the jury decided that it was inferior to a Russian entry devised by Israel Abraham Staffel, originally a watchmaker from Warsaw. The arithmometer was illustrated in the official catalogue, but it was Staffel’s calculator, already successful at a Polish exhibition and rewarded in St Petersburg, which was featured in the Illustrated London News.23
After his succession of defeats Thomas embarked on a far more active promotion of the arithmometer. His next challenge was to be the 1855 exhibition in Paris and he evidently determined to secure international victory on French soil. Thomas campaigned both through the press and in commissioned publications. He also engaged in the rituals of patronage, rituals that we might more readily associate with the decoratively elaborate calculating machines of the 18th century.
In the early 1850s Thomas distributed examples of the arithmometer to numerous crowned and titled heads of Europe. Surviving examples of these presentation machines are individually ornamented with engraved dedications on scrollwork inside the case lid.24 Thomas’s direct reward for these arithmometer gifts was a series of at least a dozen honours granted between 1851 and 1855. He was named to a stream of chivalric orders, received gold and diamond gifts in recompense for his invention and, in 1857, was elevated from Chevalier to Officer of the Légion d’Honneur.25 Aside from this personal accumulation, Thomas was able to make abundant use of these decorations in promotional material for the arithmometer, listing them to indicate the endorsements he had received from the European elite. Such efforts to raise the profile of the arithmometer placed it within a world of honour and prestige, far removed from the commercial marketplace to which the machine is usually assigned in historical accounts. Clearly the arithmometer cannot be identified as an exclusively industrial product.26
In planning for the 1855 exhibition Thomas envisioned his chief rival to be the arithmaurel which had captured so much interest at its first public appearance in 1849 (fig. 8). Subsequently awarded the prix de mécanique of the Fondation Montyon this machine had been undergoing continued development and was evidently seen as a threat to the arithmometer’s prospects. Thomas set about garnering positive publicity for his most recently developed model.
The arithmaurel and the arithmometer were juxtaposed in the pages of the Annales des Ponts et Chaussées in 1854 when each was made the subject of a separate memoir. Both reports were favourable but, apart from noting that the arithmaurel made use of the stepped cylinder which had earlier been incorporated by Thomas, there was little in the way of direct comparison.27 The stakes were raised by an 1854 article in the scientific review Cosmos, in which the abbé Moigno not only looked forward to the forthcoming exhibition struggle between the two machines but also gave his opinion of the likely outcome. Moigno moved the contest away from the staid and careful prose of official reports and presented it as journalistic high drama.28 He acknowledged his own previous championing of Maurel and Jayet but now sought to press the claims of Thomas. Not only had Thomas’s priority been overlooked but the superior potential of the arithmometer had lain unrecognised. The arithmaurel was still to be classed as a machine of the highest ingenuity. Yet Moigno reminded his readers that the best could be the enemy of the good. Maurel and Jayet had produced a powerful machine but had not yet been able to either expand its operational capacity or render it suitable for the commercial market. Thomas on the contrary had already supervised the construction of many arithmometers and there was no mechanical hindrance to the expansion of the machine’s capacity. The arithmometer may have appeared slower and more in need of human action and intelligence, but Moigno turned such evaluations on their head. The simplicity and solidity of the arithmometer identified it as the ‘classical’ instrument, representing the absolute good, while the arithmaurel was damned by its transcendence, a romantic instrument symbolising only a beautiful ideal.
Thomas presumably prompted or supported these publications in some way but, whatever the manoeuvres, they are now lost.29 His intervention is much clearer in another text from the period immediately preceding the Paris exhibition. The innocuously titled Histoire des nombres et de la numération mécanique appeared in 1855 over the name of Jacomy-Régnier, otherwise apparently best-known for a lengthy treatise on conjugal morality. Whatever expectations its title suggests, this work turns out to be a 100 page promotional puff for Thomas. Mustering not just the history of mechanical calculation but the history of arithmetic itself, Thomas is celebrated in extravagant terms. Where the surpassing acuity of a Pascal or a Leibniz had failed, Thomas had finally succeeded in creating a genuine calculating machine. Extraordinarily purple passages elevate the arithmometer to the status of a finely honed product of genius, its clarity of purpose matching a deeply considered simplicity of construction. But whereas Thomas’s achievement ought to have been the glory of the age and of the French nation, his rewards had been few and middling, with recognition bestowed more readily beyond the boundaries of France than within them.
The supply of personal anecdote and quotation reveals Thomas’s participation in this promotional venture, and its message suggests his direct support. Dark comments on the inadequacy of jury procedures witness his disappointment at previous exhibition verdicts on the arithmometer. Significantly, the only other machines to be given appreciative mention are the three which had already defeated the arithmometer. But each is quickly dispatched. Roth’s machine, although a practical device, is merely for addition. The arithmaurel rests on Thomas’s prior innovation of the stepped cylinder mechanism and is in any case both mechanically delicate and prohibitively expensive, qualities which apply likewise to the Staffel machine. Of these three, only the arithmaurel would stand as rival to the arithmometer at the forthcoming exhibi- [page 16:] tion, and Thomas had hit on a strategy to outflank this competitor.
Moigno had reported on the difficulties facing Maurel and Jayet in building an arithmaurel with a results capacity of 8 figures. Thomas faced no such problems. In the previous four years he had seen the completion of more than 200 10-figure and 50 16-figure machines.30 To drive home this advantage of capacity Thomas created a giant machine especially for the exhibition. Some 6 feet long, equipped with 15 setting sliders and 30 result dials, and encased in fine cabinetwork the result was evidently meant to capture more than technical interest (fig. 9).31
Advance reports of this calculating leviathan were already circulating before the exhibition itself. The record of a meeting of the Académie des Sciences in the pages of Cosmos again allowed the abbé Moigno the opportunity to trumpet the arithmometer’s merits. As well as citing the conclusions of recent reports he announced that Thomas’s giant machine would ‘strike a final grand blow’ against objections, resistance or inertia which might still impede the arithmometer’s progress.32
After this extensively orchestrated preparation, the initial signs from the exhibition itself were encouraging. A guidebook reported in its section on precision instruments that the giant arithmometer was the centre of lively interest. Thomas would have been satisfied to note that the arithmaurel appears only as an afterthought, an additional item also worth viewing. Yet in this moment of triumph there was a small cloud on the horizon. The same volume reported a late arrival, too recent to be properly integrated into the topically arranged text, but still justifying a mention in the national account of Sweden and Norway. No details were given other than to report that it was a quite remarkable calculating machine.33
The machine was the Scheutz difference engine. Inspired by Babbage and carried through to completion with more limited means, the second version of the Scheutz engine had been brought to London in the autumn of 1854. A working machine which could automatically calculate and print mathematical tables by the method of differences, it received Babbage’s blessing and was taken to Paris in August 1855. Despite its late arrival, the machine and its impact were widely reported. A newspaper commented, ‘we do not believe that the Universal Exposition supplies a single machine where inventive genius is more completely revealed, than the calculating machine’ of Georg and Edvard Scheutz.34
Jury and journalist were largely at one: the Scheutzes received the accolade of a gold medal, leaving the arithmometer once again with no more than an honourable mention.35 The carefully staged struggle between the arithmometer and arithmaurel had become a diverting side show rather than the main event. The arithmometer’s claims as an elevated product of genius were dismissed when faced with the powers of the difference engine. A substantial review of the exhibition quickly dealt with the two French calculating rivals before moving on to the much more astonishing achievement of the Swedish engine. With its almost intelligent qualities and its ability to replace the work of learned savants by the handle-turning operations of an ordinary man, the difference engine seemed to open up a rhapsodic world of possibilities in which intellect was overtaken by mechanism.36
Humbled once more, the arithmometer would nevertheless remain a regular entrant to subsequent exhibitions where it was duly reported and often rewarded. But never again would it be so carefully groomed for success, and yet so notably thwarted. While the exhibitions provided a dramatic public arena, their reports did however point to another dimension of the arithmometer’s public career. Beyond the realm of spectacle and rivalry the arithmometer’s performance as a commercial product was frequently noted. Here too the early news was not good.
The 1849 exhibition jury report remarked simply that the arithmometer had never entered into the commercial world, even though it could be delivered at a reasonable price. The situation was little changed by 1855 when the jury again recognised the machine’s potential to be modestly priced, even though it was as yet little known.37 By this time Thomas had distributed many examples of the arithmometer as presentation machines but he evidently expected that an increasing number of purchases would be made. Certainly, the 250 machines apparently assembled by 1854 would not all have been intended for Europe’s learned societies and royalty. But whether such completed machines had already been sold is uncertain. Apart from Moigno’s 1854 reference, the only other 19th-century source to quantify the arithmometer’s production is Sebert’s report of 1878 which records sales of 500 machines up until 1865, 300 for 1865-70, 400 for 1870-75 and finally 300 for 1875-78.38 Even by the late 1870s it would seem that no more than 100 arithmometers were being sold each year. The machine was far from being a successful object of mass production.
Advocates of the arithmometer sought to account for what they took to be its low rate of adoption and offered suggestions to expand its use. The most extended consideration of public responses to the machine was penned by the civil engineer G.-A. Hirn in 1863. Hirn offered the arithmometer as one of two inventions which had failed to achieve the public and commercial acclaim which he believed they merited (the other device was the hydrostat of Kaeppelin). His memoir was self-consciously presented as a case study in technological diffusion: having used the machine since 1855 and frequently demonstrated it to friends and colleagues he sought to document common reactions to the arithmometer and to identify and defuse the objections which he perceived as hindering its progress.39
Hirn records that after initial exclamations of wonder at the machine’s capacities, most observers first begin to doubt and then to criticise. Surely, as a machine, it must get out of order? Doesn’t it require more of an effort to learn than calculation with the pen? Won’t a user either lose the habit of calculation, or simply become mathematically lazy?40 Isn’t it restricted only to the four rules of arithmetic? How can it replace the slide rule, which has the advantage of portability?
Hirn offered practical reassurance and personal experience to allay anxieties about mechanical reliability and he presented the slide rule and the arithmometer as complementary devices, their particular strengths suited to distinct environments and calculating tasks.41 The balance of his paper was devoted to an exposition of advanced techniques which extended the arithmometer’s reach beyond the apparent restrictions of the four basic arithmetical rules.
However, Hirn suggested that most of the doubts about the arithmometer hinged on one question which every onlooker always ended by asking: how much does the arithmometer cost? Hirn acknowledged that the answer typically frightened off most enquirers. However, Thomas was not creaming off excessive profits. Rather, the elevated price arose from the machine’s manufacture process. Currently constructed one by one using hand methods, Hirn considered that the price could be halved if the machine was manufactured in quantity using the mechanical techniques of a large workshop.42
Price had been identified from the outset as a crucial issue for the arithmometer. The very first report of 1821 had worried that the arithmometer would always be an expensive device. In 1854 it was identified as the only obstacle to the wider use of the machine.43 No systematic index of the arithmometer’s price has yet been constructed, and it would in any case be complicated by the variety of different models and capacities which were available from the 1850s onwards. However, fragmentary evidence does suggest that deliberate efforts were made to cut the price of the machine.44
Users and uses: the example of England
The evidence of reports, exhibitions and contemporary comment suggests that sustained production of the arithmometer – either individually or in small batches – first began seriously in about 1850. The machine was not an overnight success. Frequently outshone in public by its rivals, it was sold at a rate of no more than 100 a year before the 1880s. The fragility of the machine’s identity and market both puzzled and disturbed advocates such as Hirn. Hirn’s memoir offered an analysis of the perceived obstacles to the diffusion of the arithmometer, much in the manner of more recent economic historians and market researchers. Can the historian do more? Even if impressionistic, Hirn had the advantage of witnessing and reporting directly on the reactions of contemporaries. Nevertheless there are sources which can complement his picture and which enable us to move from a model of passive diffusion to consider the ways in which the arithmometer was actively appropriated and adopted by users. We need to take this route if we are to understand how a device apparently so beset by problems not only survived but became the foundation for an industry. Focusing on users and their diverse uses of the machine helps to recast the problem, transforming it from the negative [page 17:] terms of ‘resistance to innovation’ and towards a more productive investigation of how the arithmometer came to figure reliably in the calculating routines of human ‘computers’.
The first report for the Société d’encouragement in 1821 noted that Thomas envisaged his machine primarily as a tool for large commercial organisations or banks. He apparently imagined that it ‘ought to render important services in counting houses, banks, exchanges, and every place where frequent and rapid calculations are necessary.’45 Doubtless this vision of the potential market was conditioned by Thomas’s own experiences both as an army administrator with the French forces in Spain and Portugal and as director of the Phénix insurance company from 1819.46
However, the exhibition reports from the 1840s and ’50s repeatedly state that the machine was not established in the commercial realm. An indication of some of the early French institutional users is given in an instruction manual of 1865 which cites the Western and Northern railways as well as the Caisse des consignations and the Creusot works.47 A post-1865 promotional leaflet suggests the expansion of the targeted market beyond commerce and finance through its references to astronomy, geometry, architecture and industry.48
In the 1850s the arithmometer was principally available from the offices of the Soleil insurance company in Paris, of which Thomas was general director. However, by at least the 1860s, agents were being appointed outside France. Exports were claimed to account for 50% of production in 1862 and 60% in 1878.49
In Germany, the arithmometer had been referred to as early as 1823,50 and its revised form was publicised in an 1862 booklet by Franz Reuleaux.51 Early satisfied purchasers included the Preussische statistische Büro, which bought its first machine in 1864 and another larger one the following year. Further pairs of machines were added in both 1878 and 1879.52 The first evidence of interest from the United States likewise comes from the 1860s and ’70s.53
The national example I want to focus on is, however, that of England, principally for the pragmatic reason of access to archives and sources. The arithmometer was known in England at least as early as its 1851 appearance at the Great Exhibition. As well as his support in the pages of Cosmos and despite his faltering command of English, the abbé Moigno demonstrated an example at the 1854 meeting of the British Association.54 Although it is clear that a few arithmetical adventurers purchased machines in the 1850s,55 it is primarily for the 1860s and later that we have detailed evidence of the use of the arithmometer.
A London-produced promotional leaflet provides one of the most vivid windows onto the arithmometer’s use in England. After describing the machine and noting its exhibition awards – most recently at Moscow in 1872 – the leaflet prints a list of the machine’s users. A total of 33 corporate bodies, from government departments to colleges, observatories and insurance companies, are included, followed by 40 individuals and firms representing engineers, bankers, actuaries, doctors and chemists.56 The 1872 list was evidently intended to demonstrate that the arithmometer had already arrived, and that it was well-established in a wide range of professional pursuits. But by naming a series of exemplary owners in order to persuade prospective customers this leaflet provides a point of entry to a rich network of users.
The 1872 list names ‘Mr. Brunel, C.E., Westminster’, who can be readily identified as the engineer Henry Brunel – son of Isambard Kingdom Brunel. In March 1866 Brunel wrote to a correspondent:
I have just got what my mother irreverently calls ‘a new toy’ – to wit a calculating machine price £12 which does all the common operations of arithmetic viz addition, multiplication, subtraction & division in the twinkling of an eye. It is really a very useful article worth its weight in brass.57
Later the same month, the machine – still described as ‘very useful’ and now identified as French – was recommended to another correspondent.58 From a subsequent letter it appears that Brunel’s machine had been ordered for him by his engineer colleague William Froude,59 and it was to Froude that Brunel reported in May of ‘the grand use of my calc. machine this afternoon getting out some quantities’. The context of the letter suggests that Brunel sought arithmetical aid as he worked on a tunnelling machine scheme for the proposed Channel Tunnel.60
Confirmation that Brunel’s calculating machine was indeed the arithmometer and that it was treated as more than just a passing novelty comes in the following year. Brunel had evidently persuaded Froude to take a closer look at was presumably a new model and had asked Thomas’s London agent to make the ‘Arithmetic Machine’ available. That the service may have been performed before, though not entirely to Brunel’s satisfaction, is suggested by his afterthought: ‘Please make sure that the key of the box is sent with it.’61 If Froude had not actually bought the machine previously, Brunel’s enthusiasm was infectious: Froude’s name also appears on the 1872 list of the arithmometer’s purchasers.
By 1868 Brunel had learnt to call the machine an arithmometer and was ordering another example. He immediately reported his acquisition in terms which suggest both his intimate familiarity with the machine and also the way in which its capacity and power had become a matter of friendly rivalry: ‘I have a £20 Calc: Machine as big as Clarke’s with a fizzer for the little beggars’.62 As the more prosaic language of the order makes clear, Brunel’s ‘fizzer’ was the eraser knob and mechanism for the small quotient dials, introduced in 1865.63
The evidence of Brunel’s correspondence indicates how, beneath the outward face of anonymous market phenomena and purchase decisions, personal friendships and recommendations were vital in fostering the commercial success of the arithmometer. Moreover, his enthusiastic efforts help us to rethink the character of the machine’s ‘diffusion’. Brunel demonstrates the extent to which users were more than mere passive vectors for the spread of an unchanging object. Writing to the agent in 1868 to enclose his delayed payment, Brunel listed four faults in the machine which could be remedied without great trouble. The last of them – concerning the operation of the setting sliders – was simple to correct at the manufacturing stage but troublesome afterwards and had afflicted the four most recent of the five machines bought by Brunel and his friends.64
Brunel’s suggestions were not warmly received. Writing from Froude’s in March 1869 he remarked that ‘I now get my Arithmometers through Adie my Instrument Maker as the regular agent did not take pains to serve me well’. Bypassing the agent, Brunel got Adie to buy directly from Paris and then to make alterations according to his preferred pattern, as well as adding a leather carrying case. By this stage Brunel was acting as an intermediary himself, obtaining his ‘improved’ arithmometers through Adie and then sending new machines to friends while also receiving damaged or worn examples for repair. It should perhaps be no surprise that Hawkshaw and Noble, two of the engineers with whom Brunel carried on his traffic in arithmometers, also appear in the 1872 list of purchasers.65
In addressing problems with his friends’ machines, Brunel was led into highly detailed examinations of their mechanisms. Mechanical defects which jammed the machine could be diagnosed and repaired but more worrying were instances when the machine was found to be giving the wrong results. Errors of this kind undermined the trust on which regular operation was founded. Brunel therefore went to great lengths to identify the sources of such subtly unsettling faults. In one instance, with the help of diagrams and much explanation, he tracked down a problem to wear and tear in the carrying mechanism, but only when the carriage was in one particular position.66 Such faults could have cast a long shadow over the reliability of the arithmometer among isolated users but, by capturing the fault, devising a remedy and passing it on to correspondents, Brunel helped to keep the machine above the level of unrecoverable suspicion. In doing so he helped to build up a repertoire of cautions, tricks and fixes well beyond the more anodyne recommendations of the official instruction manuals.
Henry Brunel enables us to recover the network of active interest through which the arithmometer’s engineering trajectory was accomplished. While the purchase of other machines can be documented, in the present state of research it often remains difficult to identify particular motivations. For example, the 1872 list includes the South Kensington Museum; the corresponding machine, purchased in 1868 and marked for the Science and Art Department, survives in the Science Museum, London.67
Other personal connections are occasionally hinted at. Both the Cambridge Observatory and Professor Bashforth appear in the 1872 list. John Couch Adams, director of the Cambridge Observatory from 1861, is reported to have remarked that an arithmometer was ‘in constant use there in the observatory, and that [page 18:] it is most valuable in shortening the tedious processes of astronomical calculations’.68 Bashforth was second wrangler at Cambridge in 1843 when Adams was senior wrangler and they became close associates, collaborating on a treatise on capillary action as late as 1883. However, after his appointment as professor of applied mathematics at Woolwich in 1864, Bashforth’s primary interest lay in ballistics. In reducing the results of experiments with his chronograph and in calculating ballistic tables, Bashforth relied on the arithmometer as ‘a most valuable assistant’.69
One of the most prominent areas in which the arithmometer came into use in England was in insurance. Actuaries were probably the first professional group to adopt it and adapt their work to its capabilities. From the 1860s there was a steady stream of articles showing how the specialised and repetitive calculations required to construct actuarial tables could be reworked to take advantage of features of the arithmometer. More than just exposition, there was also active debate about the merits of machine calculation.70 The 1872 list illustrates the extent to which insurance companies were not just considering the possibility of adopting arithmometers but were already making their purchases. A total of 17 offices had already bought machines from the London agent. Nor do such references necessarily represent only a single machine. Among those listed was the Prudential, which underwent dramatic expansion from the mid-1860s as it pioneered mass ‘industrial insurance’ beyond the socially elevated market to which companies had largely restricted themselves. The company’s investment in, and reliance on, the arithmometer spiralled as its business grew. Aside from daily calculation, the arithmometers were put to work when the company fulfilled its legal obligation to conduct quinquennial valuations of every policy. The 1877 valuation took 300 clerks 6 months to complete and it was reckoned that, with about 2.5 million policies in force, 4,635,894 calculations were carried out. The Prudential’s Henry Harben recorded that ‘We had 24 arithmometers at work on the business, and without them it would have been impossible.’71
Essential as the arithmometer was becoming to the Prudential’s business, the machine could not be treated as a fully reliable resource. The company’s archives preserve a few fragmentary but revealing records of repair work carried out on their arithmometers during the 1870s. Springs would snap and other more serious mechanical defects were not uncommon. The effort of the quinquennial valuation severely tested the machines’ robustness: in one month alone in 1877 12 machines required attention for one or more repairs.72 To guard against the dangers of both operator and mechanical error, the Prudential typically carried out its calculations in parallel, using one machine to check the results of another.73 But the company was so concerned with guaranteeing reliability that it sponsored the development of an English version of the arithmometer in the hope of obtaining improved performance. An 1879 letter to The Times announced ‘a premium of £300 in addition to the full price of 20 perfect English-made machines’. When the prize was paid in January 1882, £200 went to the instrument makers Elliott Brothers.74
The Prudential’s initiative was evidently born of frustration at the perceived inadequacies of a device that they could no longer do without, a device they had built into their administrative procedures. Henry Brunel’s response to his similar experience had been to commission his regular instrument maker to carry out alterations. But government departments also faced the same problems with which commercial bodies and individual engineers were struggling.
In the history of computing the General Register Office (GRO), Britain’s centre for official statistics, is known for commissioning the third Scheutz difference engine, manufactured by Bryan Donkin & Co. and delivered in 1859.75 Although this machine assisted in the calculation and printing of William Farr’s English Life Table (1864), it was afterwards decommissioned and placed in storage. The GRO turned away from the ambitions of the difference engine to the more limited means of the arithmometer.
Treasury letters record the GRO’s purchase of arithmometers in 1870, 1872, 1873 and 1877 and, although the utility of the machine was repeatedly reported and endorsed, qualifications were entered from the beginning. The first letter seeking authorisation for purchase asked not for the price of the machine (£20) but for £25: ‘some improvements have been suggested after trial and experience in this Department, which may cost perhaps some two or three pounds additional’.76 Like Brunel, and perhaps because of his example, custom alterations were seen to be necessary before delivery. Such improvements were not however enough to render the machines fault-free, and running repairs were still required. Although it was ultimately left to the Prudential’s private initiative, the GRO considered the same chauvinistic solution later sponsored by the insurance company. Responding to Treasury enquiries, the GRO took the view that ‘the liability of “Arithmometers” to get out of order and their noise would be greatly diminished if they were made by more accurate and better workmen - perhaps Englishmen’.77
The Treasury did not however resort to offering English incentives but hoped to prevail upon the current manufacturer. Having received another report in 1873 from Sir Francis (later Lord) Sandford on a machine supplied to the Education Department, the Treasury suggested that Sandford and the GRO should together ‘communicate with the Inventor of the “Arithmometer” in order to ascertain if improvements could not be introduced in the construction of these machines’.78 Thomas had died in 1870 and English government efforts to encourage new developments met with no more success than Brunel’s. Four years later the GRO addressed the need for improvements in the machine: ‘this has been frequently represented to the manufacturers in France and to their Agents in this Country, but the reply is that the demand for them is so limited that no alteration can be made in them; consequently they frequently require repairs.’79 This remarkably telling comment indicates that the machine was offered as being ‘good enough’; despite the importunities of unruly English users the arithmometer’s manufacturers did not think that it merited further investment and development.
The introduction of an English-made arithmometer in the 1880s was evidently meant to capitalise on the dissatisfied sentiments of English users of the Thomas machine. Later GRO documents show how the comparison between the Thomas arithmometer and its English competitor was analysed, playing off cost against long-term reliability.80 But rather than continuing with this story and highlighting the frailties of the arithmometer I want to conclude my account of English users by returning to the early 1870s.
The 1872 list of purchasers brings together companies and individuals from many fields. I have shown how engineers, astronomers, actuaries and statisticians engaged with the machine, celebrating its utility and actively probing its weaknesses. Was the juxtaposition of these different intellectual and professional roles merely an artefact of a promotional leaflet? Did the arithmometer move along parallel but distinct tracks in the professionalising world of later 19th century England?
A meeting of the Society of Telegraph Engineers in April 1872 suggests that the links among advocates and users of the arithmometer were not constrained by disciplinary or professional boundaries. The Society gathered to hear a paper on ‘the application of the calculating machine of M. Thomas de Colmar to electrical computations’ by Thomas T.P. Bruce Warren. The paper reveals the extent to which Warren had taken his cue from recent accounts of the actuarial use of the arithmometer; actuaries had pointed the way in showing how calculating procedures should be reworked in order to benefit from the capabilities of the machine. Perhaps even more significant is the printed discussion which follows the published version of the paper.81 The contributing audience did not consist of a narrowly bounded group of telegraph engineers, or indeed electricians defined more broadly. General Hannyngton of the India Office, one of the prime actuarial proponents of the arithmometer, was present and his views were supplemented by those of Henry Harben, the secretary of the Prudential. Another actuary to speak up was Peter Gray and comments also came from Dr Royston Piggott F.R.S. All of these figures and their institutions are recorded in the 1872 list. The discussion ranged from electrical work through actuarial experience to trigonometrical and surveying issues, as well as the handling and maintenance of the machine.
The judgement of Siemens, the Society’s President, captures the effect of this informed cross-disciplinary audience in persuading new users of the arithmometer’s potential. Siemens confessed that he had initially had doubts about the suitability of the arithmometer as a topic for his society’s meeting. ‘But the more he had seen and heard about it, the more he was satisfied the subject was one of great interest to Telegraph Engineers; they had so much to do with calculations of an intricate kind.’ [page 19:]
Conclusion
I began by citing a widely-held view of the arithmometer as the first commercially manufactured calculating machine. While my account casts doubt on less cautious claims (such that it was the first mass-produced calculator),82 that initial general statement remains intact as a concise caption for the arithmometer – though only for the developed form available towards the end of Thomas’s long life. Thomas’s business success in insurance meant that the low rate of machine production and its apparent lack of profit were not problems which need have troubled him.83 On the contrary, Thomas advertised his extraordinary investment. In his promotional book of 1855, Jacomy-Régnier announced that Thomas had spent 300,000 francs on developing the arithmometer, setting that figure against Leibniz’s reputed costs of 100,000 francs and Babbage’s notorious government subvention of £17,000 (reckoned as equivalent to 425,000 francs).84 If we are to label Thomas’s work on the arithmometer, it is more likely to fall within the category of vanity publishing than mass production.
The burden of this paper has been to examine the lengthy and complex process by which the arithmometer’s eventual success was achieved – if indeed the process was ever completed. At the end of my period, in the late 1870s, it is clear that the arithmometer occupied an increasingly established and tangible calculating niche but, while its usefulness was praised, a search was already underway for a superior replacement. The perceived need for an alternative was taken as a symptom of the arithmometer’s inadequacies, but the assumption that the desired replacement should be functionally (and even visually) identical can equally be interpreted as a mark of the machine’s success.
Clearly it is not enough to date the arithmometer to 1820 and then interpret its subsequent history as simply a question of diffusion. The mechanical and public identity of the machine was worked and reworked, and its users adapted not just their own computing work but altered the machine itself. These three elements – the machine’s development as a mechanism, its public evaluation and reputation, and the activities of its users – do not exhaust the history of the arithmometer: the details of its manufacture, for example, are still largely obscure. Nevertheless, only by jointly attending to the diverse elements of the arithmometer’s persona can we can begin to grasp the machine’s career, from fragile prototype to de facto standard.
Acknowledgements
I would like to thank the Scientific Instrument Society for supporting this work with a research grant. Many individuals – too many to list here – have helped by supplying information on individual machines or allowing access to their collections. Particular thanks are due to Michel Bardel, Paolo Brenni, Dominique Brieux, Judit Brody, Friedrich Kistermann, Doron Swade, Peter Traynor and Geoffrey Tudor. I would especially like to thank Robert Otnes for prompting me to begin this work many years ago and for his generosity in subsequently passing on the results of his own research.
Stephen Johnston
Museum of the History of Science
Broad Street
Oxford OX1 3AZ
stephen.johnston@hsm.ox.ac.uk
Notes
1. See, respectively, D. Baxandall and Jane Pugh, Calculating Machines and Instruments: Catalogue of the Collections in the Science Museum (London, 1975), p. 11, Uta C. Merzbach, Georg Scheutz and the First Printing Calculator (Washington, 1977), p. 37 and Michael Lindgren, Glory and Failure: the Difference Engines of Johann Müller, Charles Babbage and Georg and Edvard Scheutz (Cambridge, Mass., 1990), p. 290. For further references, among many others, note Michael R. Williams, ‘Early calculation’, in William Aspray (ed.), Computing before Computers (Ames, 1990), p. 50 and Gerard L’E. Turner, Nineteenth-Century Scientific Instruments (London, 1983), p. 283.
2. Jean Marguin, Histoire des instruments et machines à calculer (Paris, 1994), pp. 83-9.
3. Published in the Bulletin de la Sociéte d’encouragement pour l’industrie nationale (hereafter Bulletin). For this and other arithmometer articles from the Bulletin I cite page numbers from the reprinted versions published in celebration of the machine’s centenary in 1920, while also giving the year of first publication. The report by Sebert was dated 13 December 1878, Bulletin (1879/1920), 694-720, p. 707. The centenary issue of the Bulletin was the major source for Ernst Martin’s account of the arithmometer in The Calculating Machines (Die Rechenmaschinen): their History and Development, trans. and ed. by Peggy Aldrich Kidwell and Michael R. Williams, Charles Babbage Institute Reprint Series for the History of Computing, 16 (Cambridge, Mass., 1992), pp. 53-7.
4. Hartmut Petzold, Rechnende Maschinen: eine historische Untersuchung ihrer Herstellung und Andwendung vom Kaiserreich bis zur Bundesrepublik, Technikgeschichte in Einzeldarstellungen, 41 (Düsseldorf, 1985), p. 102. For the English machines of Tate and Edmondson see Baxandall and Pugh (note 1), p. 12.
5. Patent no. 1420, 18 November 1820. Thomas’s letter of request to the Minister of the Interior, dated 6 October 1820, is reproduced in J. Joly, ‘Un grand inventeur alsacien: Charles-Xavier Thomas’, La Vie en Alsace, p. 132. This article is the most authoritative biographical source on Thomas and a copy was kindly supplied by Friedrich Kistermann. I have not yet verified the date of the article but it must have appeared in the Strasbourg periodical in 1935 or shortly afterwards, when a monument to Thomas was erected in Colmar (see Maurice d’Ocagne, ‘Thomas de Colmar, inventeur de l’arithmomètre’, Revue scientifique, 73 (1935), 783-5).
6. The arithmometer was first examined by Bréguet and Francoeur, and Francoeur’s report of 26 December 1821 is Bulletin (1822/1920), 660-2. The subsequent memoir by Hoyau is ibid., 662-70.
7. NMAH, Washington, inv. 326,649. This machine, or one very like it, was exhibited by Darras, the then manufacturer of the Thomas arithmometer, in the 1920 exhibition celebrating the centenary of the arithmometer: see Bulletin (1920), pp. 620-1.
8. On Devrine, G.H Baillie, Watchmakers and Clockmakers of the World, 3rd ed. (London, 1951/1966), p. 84 lists him as Paris, 1824, though Tardy, Dictionnaire des horlogers français, part 1 (Paris, 1971), p. 184 gives only a later reference to a Devrine at the Galerie Vivienne in 1870. Devrine also made instruments: the Musée des Arts et Métiers has a balance bought from him in 1809 (inv. 168). The existence of this machine, and Devrine’s role in its manufacture, creates a problem for any attempt to identify the early arithmometer as a radical break with the past. Cf. Annegret Kehrbaum and Bernhard Korte, Calculi: Bilder des Rechnens einst und heute/Images of Computing in Olden and Modern Times (Opladen, 1995): ‘Thomas’s machine also inaugurated a new epoch in the technical production of calculating machines. In the past practically all calculating machines had been made by watchmakers ...’ (p. 70). To further reinforce the point, note that d’Ocagne (note 5, p. 785) states that Thomas was initially helped by Piolaine, ‘un jeune ouvrier horloger de Neuilly-sur-Seine’. I have been unable to confirm this independently, but note that Tardy (part 2 (Paris, 1972), p. 523) lists a member of the Piolaine family at Neuilly-sur-Seine in 1838 and Baillie has Piolaine fils at Paris in 1825 (p. 253). (Note added 24 March 2005: an article in L'Illustration of 20 October 1849 provides the evidence for Piolaine’s involvement. Piolaine, described as ‘un jeune homme ... fils d’un horloger de Neuilly’, was working on a new machine when he died unexpectedly in 1848. See either an extract of the article, or a scan of the full text.)
9. The circular design of the patent’s multiplicateur recalls Leibniz’s machine. Although often considered to have been lost to view for almost 200 years, images of Leibniz’s calculating machine were available in the 18th century; see the 1744 engraving in Kehrbaum and Korte (note 8), p. 61.
10. Instruction pour se servir de l’arithmomètre (Paris, 1852; facsimile edition by Alain Brieux, Paris, 1982), preface, p. 2. The claim was accepted and promoted. The abbé Moigno, Cosmos, 4 (1854), p. 76 writes extravagantly and implausibly of Thomas ‘qui, depuis trente ans, n’avait pas cessé un seul instant d’améliorer son oeuvre’. Equally, the contemporary report in the Comptes Rendus Hebdomadaires des Séances de l’Académie des Sciences, 39 (1854), 1117-24, p. 1123, writes that ‘Quant à l’arithmomètre, qui ne se trouve pas encore dans le commerce, c’est avec le plus honorable désintéressement que, depuis trente ans, M. Thomas n’a cessé de le perfectionner pour le rendre utile, de simplifier pour qu’il pût être livré à un prix modéré’.
11. See Joly (note 5) and note that Thomas’s name features repeatedly in P.J. Richard, Histoire des institutions d’assurance en France (Paris, 1956).
12. For 1844, [Exposition des produits de l’industrie française en 1844], Rapport du jury central (Paris 1844), II, p. 504. A machine dated 1848, again the property of Darras, was displayed at the arithmometer centenary exhibition (note 7), pp. 620, 622. What was presumably the same machine was offered at Drouot-Richelieu, Paris, 17 November 1995, lot 124; its present whereabouts are unknown. [page 20:]
13. Patent no. 6261, 8 December 1850; addition, 19 August 1851. An English patent to the same effect was taken out in 1851, no. 13,504.
14. Cf. Bulletin, 51 (1852), p. 615.
15. An 1851 report for the Société d’encouragement by Benoît remarks in a footnote that, without expanding the size of the arithmometer, it should be possible for the machine to record quotients on special dials: Bulletin (1851/1920), p. 691. The addition to the 1850 patent (note 13), filed a few months after Benoît’s report, suggests a complex mechanism for recording quotients which never seems to have been implemented. Note that a machine of c. 1851 in the Musée des Arts et Métiers, Paris (inv. 40571) has a series of independent dials on the setting plate, without any mechanical connection, on which partial quotients could have been manually inserted.
16. Sebert (note 3), p. 703. Note however that the 1855 exhibition machine discussed below already had quotient dials.
17. Francoeur (note 6), p. 661, Comptes Rendus (note 10), p. 1120, Sebert (note 3), p. 698.
18. For example, Rapport du jury central sur les produits de l’agriculture et de l’industrie exposés en 1849 (Paris, 1851), II, 549-1, p. 550.
19. Comptes Rendus (note 10) and ibid., 38 (1854), p. 315. Thomas also attempted to enter the arithmometer for the Académie’s prix de mécanique in this year but the entry was deferred until 1855: ibid., 39 (1854), p. 1221. The machine, with an engraved dedication to the Académie, survives in the Musée des Arts et Métiers, inv. 7479.
20. Marguin (note 2), p. 111: ‘Pendant un demi-siècle, la machine y régna seule.’
21. For Thomas and Roth at the 1844 exhibition, see the jury report (note 12), II, pp. 503-4. The catalogue of the Bibliothèque Nationale lists Roth’s published leaflets on his adding machine. The report on Roth’s adding machines and counters appeared, along with a historical classification of calculating devices, in Bulletin (1843/1920), 673-84. The exhibition guide mentioning Roth is Jules Burat, Exposition de l’industrie française année 1844. Description méthodique, 2 vols (Paris, n.d.), I, pp. 60-2. Roth (whose first name is also given as David) appears in Marguin (note 2), which illustrates both his adding and his (unfinished) calculating machines (pp. 114-7).
22. See note 18.
23. [Exhibition of the Works of Industry of All Nations, 1851], Reports by the Juries (London, 1852), p. 310. Illustrated London News, Exhibition Supplement, 20 September 1851, pp. 354-5.
24. An 1850-style example dedicated to Marie-Thérèse Louise de Bourbon, regent of the duchies of Parma and Plaisance, was offered at Drouot-Richelieu, Paris, 10 May 1990, lot 114. Another presentation machine, probably from after 1852 judging by the form of the add/subtract switch, is in the Heinz Nixdorf MuseumsForum, Paderborn, inv. no. E-1994-681. A more modest level of decoration was reserved for personal presentations rather than those destined for the crowned heads of Europe; see the example dated 22 July 1852 and dedicated to Mme Zenoïde de Jacquemain, ‘souvenir affectueux de l’Inventeur’ (Museon, The Hague, inv. 9006; http://museon.museon.nl/objecten/567.htm). Presentation examples were still being offered after Thomas’s death by his son: see Bulletin (1920), p. 625 for the machine offered to the emperor of Brasil in 1872 by Thomas de Bojano.
25. Thomas had been created Chevalier of the Légion d’Honneur in 1821, for his military service rather than the arithmometer (Joly, note 5, p. 131).
26. For an account stressing the industrial character of the arithmometer and contrasting it with impractical earlier machines destined only for the collections of princes and nobles, see Kehrbaum and Korte (note 8), pp. 70, 64.
27. On the arithmaurel, see Lalanne in Annales des Ponts et Chaussées, 3rd ser., 8 (1854), 2nd trimestre, pp. 287-310. Lemoyne’s report on the arithmometer directly follows at pp. 311-332; its reference to Maurel and Jayet comes at the end of a historical review on p. 328.
28. F. Moigno, ‘Arithmomètre ou machine à calcul’, Cosmos, 4 (1854), 72-9. A descriptive account of the arithmometer also appeared in a subsequent number of Cosmos: 4 (1854), 186-96. Moigno was one of the leading vulgarisateurs of science, emphasising spectacle and controversy rather than ‘normal science’; see Susan Sheets-Pyenson, ‘Popular science periodicals in Paris and London: the emergence of a low scientific culture, 1820-1875’, Annals of Science, 42 (1985), 549-72, pp. 556-7.
29. Robert Fox, ‘Edison et la presse française à l’exposition internationale d’électricité de 1881’, in his Science, Industry, and the Social Order in Post-Revolutionary France (Aldershot, 1995) has shown how big business interests were able to buy influence and favourable press coverage on a massive scale at the electricity exhibition of 1881. Thomas may have pursued similar tactics, but on a much smaller scale.
30. Cosmos, 4 (1854), p. 77.
31. The machine remained with the firm and is listed in a 1915 inventory of materials and machines drawn up for Darras: ‘Grande machine à calculer d’Exposition 1855 dans son grand meuble en bois noir incrusté et garni de cuivre fabriquée par M. Thomas de Colmar. Prix réduit convenu 1.000 [francs]’ (inventory copy in Mathematics Files, National Museum of American History, Washington). Darras exhibited the machine at the 1920 exhibition, Bulletin (1920), pp. 621, 623. It is now in the collection of IBM: A Calculator Chronicle: 300 Years of Counting and Reckoning Tools (Armonk, n.d.), pp. 14-15.
32. Cosmos, 5 (1854), p. 663.
33. H. Tresca (ed.), Visite à l’Exposition Universelle de Paris, en 1855 (Paris, 1855), p. 353 (arithmometer and arithmaurel) and p. 25 (Swedish machine).
34. On the Scheutz engine, see Lindgren (note 1). The engine’s year-long stay in Paris is discussed on pp. 193-203 and the newspaper citation is on p. 196.
35. [Exposition Universelle de 1855], Rapports du jury mixte international (Paris, 1856), p. 405.
36. Léon Brisse, Album de l’Exposition Universelle, 3 vols (Paris, 1856-9), II, p. 194.
37. Rapport (note 18) II, p. 551 and Rapports (note 35), p. 405.
38. Sebert (note 3), p. 704. Sebert’s figures have provided the primary foundation for the few existing analyses of factors affecting the production and adoption of the arithmometer. See Ludolf von Mackensen, ‘Bedingungen für den technischen Fortschritt: dargestellt anhand der Entwicklung und ersten Verwertung der Rechenmaschinenerfindung im 19. Jahrhundert’, Technikgeschichte, 36 (1969), 89-102 and F.W. Kistermann, ‘The slow acceptance of mechanical calculating machines – some reflections and remarks’, Proceedings of the Cultural History of Mathematics, 6 (1996), 32-43. The only independent way of assessing the reliability of the data of Sebert and Moigno is by studying surviving machines and their serial numbering system. Preliminary indications suggest that Sebert’s figures tally reasonably well with machine serial numbers. What is not yet clear is whether the serial numbers provide a reliable guide to the number of machines actually constructed. An unknown number of examples from the early 1850s do not carry serial numbers. Nor is it clear that serial numbers were assigned in a continuous sequence. Such issues will only be clarified when a more comprehensive survey of surviving machines has been carried out.
39. G.-A. Hirn, ‘Notice sur l’utilité de l’arithmomètre et de l’hydrostat’, Annales du Génie Civil, 2nd part, 2 (1863), 113-7, 152-64.
40. This fear had been expressed by the Royal Academy of Sciences in Madrid, whose report on the arithmometer had worried about the social consequences of the machine’s widespread adoption. Thomas once more relied on the journal Cosmos, presumably in the person of the abbé Moigno, to vigorously rebut this view: Cosmos, 5 (1854), pp. 660-1.
41. Earlier reports had already concluded that the arithmometer had an important place alongside rather than as a replacement for existing technologies such as slide rules and logarithmic tables. See, for example, Lemoyne (note 27), esp. pp. 320-3.
42. Lemoyne (note 27), p. 329 had already considered that, if 10,000 examples were to be commissioned, the machine could be built for less than 100 francs, instead of its then current price of 300. Hirn’s half-price comment was later repeated in Sebert (note 3), p. 707.
43. Francoeur (note 6), p. 661 and Lemoyne (note 27), p. 329.
44. In 1856 the arithmometer was included among the recommended specialities advertised on the inner leaves of Cosmos. 10-figure machines (5x0x10) were priced at 250fr, and [page 21:] 16-figures (8x0x16) at 500fr. Franz Reuleaux (note 51, p. 40) complained of the high price of the machine in 1862 but the prices he quotes are significantly less than in 1856: the same 10 and 16-figure machines were now only 150fr and 300fr respectively. Additional models were also available to Reuleaux, though the most expensive was still only 400fr.
45. Francoeur (note 6), p. 661.
46. Joly (note 5), pp. 130-1.
47. Instruction pour se servir de l’arithmomètre (Paris, 1865). Copy with arithmometer in Národní technické muzeum, Prague, inv. no. 6337. The 1852 booklet (note 10) mentions only Benoît, who produced the 1851 report on the arithmometer for the Société d’encouragement. Sebert’s report of 1878 provides some additional names (note 3), p. 707.
48. Reproduction included with entry for inv. M559 in the loose-leaf catalogue of the Brunsviga collection (copy in Mathematics Collection files at Science Museum, London).
49. [Exposition Universelle de 1862 à Londres], Section Française: Catalogue Officiel (Paris, 1862), p. 109 and Sebert (note 3), p. 704.
50. Dinglers polytechnisches Journal, 11 (1823), p. 121f., cited by von Mackensen (note 38), p. 100.
51. Franz Reuleaux, Die Thomas’sche Rechenmaschine (Freiberg, 1862). The pamphlet was extracted from Reuleaux’s article in Der Civilingenieur, 8 (1862). The piece was also republished in Dinglers polytechnisches Journal, 165 (1862), 334-62 and a second edition appeared in 1892.
52. Petzold (note 4), p. 106. For the use of the arithmometer in trigonometrical tabulations, see August Junge, Tafel der wirklichen Länge der Sinus und Cosinus (Leipzig, 1864), preface.
53. Peggy Aldrich Kidwell, ‘American scientists and calculating machines – from novelty to commonplace’, Annals of the History of Computing, 12 (1990), 31-40, pp. 32-4.
54. Report of the Twenty-Fourth Meeting of the British Association for the Advancement of Science; held at Liverpool in September 1854 (London, 1855), ‘Notices and abstracts of miscellaneous communications to the sections’, pp. 1-2 and Cosmos, 5 (1854), pp. 463-4.
55. In the discussion following C.V. Boys, ‘Calculating machines’, Journal of the Society of Arts, 34 (1886), p. 387, Thomas Ackland mentioned that he had bought a Thomas machine in 1851.
56. Copy in Mathematics Collection Technical File inv. 1980-1779, Science Museum, London. The leaflet can be dated to either 1872 or 1873 from its reference to an as-yet-unpublished paper given at the Society of Telegraph Engineers (discussed below). I shall refer to it as the ‘1872 list’.
57. Brunel to Adams, 18 March 1866, Bristol University Library, Brunel Collection, Letter Book VII, f. 106 (hereafter Brunel Collection).
58. Brunel to J. Dobson, esq., 27 March 1866, Brunel Collection, VII, f. 15.
59. Brunel to de Fontaine Moreau, 13 July 1868, Brunel Collection, IX, f. 115.
60. Brunel to Froude, 31 May 1866, Brunel Collection, VII, f. 157.
61. Brunel to L. de Fontaine Moreau, 26 November 1867, Brunel Collection, VIII, f. 326. Brunel wrote to Froude about the arrangement on the same day; ibid., f. 322.
62. Brunel to Gamble, 14 June 1868, Brunel Collection, IX, f. 99.
63. Brunel to L. [de] Fontaine Moreau, 10 June 1868, Brunel Collection, IX, f. 97.
64. Brunel to de Fontaine Moreau, 13 July 1868, Brunel Collection, IX, ff. 114-5.
65. Brunel to Captain Noble, 10 March 1869, Brunel Collection, IX, f. 237. The 1872 list is apparently mistaken in assigning Captain Noble to the Postal Telegraph Offices. Brunel addressed Noble at Armstrong’s Elswick Works at Newcastle; on Noble see David J. Jeremy, Dictionary of Business Biography, 5 vols (London, 1984-5), IV, pp. 444-6. For Adie, see Brunel to Adie, 28 December 1868, Brunel Collection, IX, f. 169 and 11 March 1869, Brunel Collection, IX, f. 236. Adie is Patrick Adie, who began a London offshoot of his father’s Edinburgh business in 1844: T.N. Clarke, A.D. Morrison-Low, A.D.C. Simpson, Brass & Glass (Edinburgh, 1989), pp. 75-84.
66. Brunel to Captain Noble, 29 April 1869, Brunel Collection, IX, f. 284.
67. Science Museum, Mathematics Collection, inv. 1868-1. The machine is engraved ‘S. & A. D. S.K. MUS.’ Kevin Johnson kindly confirmed from the museum archives that the machine was bought in Paris on 11 January 1868 for £16.
68. Transactions of the Devonshire Association for the Advancement of Science, Literature and the Arts, 7 (1875), p. 174. I owe this reference to Jackie Britton. The Cambridge Observatory was listed as a purchaser in the 1865 edition of the instruction manual (note 47).
69. For Bashforth, see Dictionary of National Biography, 1912-1921, pp. 35-6. The reference to the arithmometer appears in his Supplement to a Mathematical Treatise on the Motion of Projectiles (London, 1881), p. 126.
70. Andrew Warwick, ‘The laboratory of theory, or what’s exact about the exact sciences?’, in M. Norton Wise (ed.), The Values of Precision (Princeton, 1995), 311-351, pp. 329-31.
71. Cited by Martin Campbell-Kelly, ‘Large-scale data processing in the Prudential, 1850-1930’, Accounting, Business and Financial History, 2 (1992), 117-139, p. 123.
72. Prudential Assurance Company, Calculating Machine Papers. Prudential-owned arithmometers from the 1870s still survive: see figure 1.28 in Williams (note 1), p. 50.
73. Henry Harben in the discussion to Thomas T.P. Bruce Warren, ‘On the application of the calculating machine of M. Thomas de Colmar to electrical computations’, Journal of the Society of Telegraph Engineers, 1 (1872), p. 165.
74. For the Times letter, see Campbell-Kelly (note 71), pp. 127-8. Payment is recorded in the Prudential Assurance Company Board Minutes, 19 January 1882. Several arithmometers signed by Elliott Brothers survive, for example, Science Museum, London, Mathematics Collection, inv. 1989-636.
75. On this engine, see Lindgren (note 1), pp. 211-35. Note that Donkin’s name appears on the 1872 arithmometer list.
76. Public Record Office (PRO), RG/29/2/111, 29 January 1870. I am indebted to Doron Swade for providing me with transcripts of this and other Treasury-GRO documents.
77. PRO RG29/2/162, 28 July 1873.
78. PRO RG29/6/109, 5 August 1873. On Sandford and his career in the Education Department, see the Dictionary of National Biography.
79. PRO RG29/2/250, 16 March 1877.
80. PRO RG29/3/129 and RG29/7/80 from 1893 and cf. Boys’s paper (note 55) which compares English arithmometers with the inferior workmanship of the Thomas machine.
81. Warren (note 73). The paper is pp. 141-164 and the discussion appears at pp. 164-8. Warren was electrician to Hooper’s Telegraph Works, who appear in the 1872 list.
82. Stan Augarten, Bit by Bit: an Illustrated History of Computers (London, 1984), pp. 37-8.
83. Cf. Hirn (note 39), p. 113 on the machine’s relative lack of profitability.
84. Jacomy-Régnier, Histoire des nombres et de la numération mécanique (Paris, 1855), pp. 28, 58, 68.