Chapter 2
THOMAS DIGGES
Gentleman and mathematician
1. THE IDENTITY OF THOMAS DIGGES
Of all the characters who figure in this study, Thomas Digges (c.1546-1595) is the best known, certainly within the history of science. His standing rests principally on a short text, the Perfit Description of the Celestiall Orbes (1576), which translates, adapts and extends the principal cosmological passages from Book 1 of Copernicus’s De Revolutionibus (1543). Since the 1930s, when the Perfit Description was reprinted and its historical significance proclaimed, Digges has been identified as the first public advocate of Copernicanism in England. He has therefore repeatedly been given at least a bit part in the story of Copernican astronomy and, by extension, in the larger tale of the Scientific Revolution.1 [page 51:]
But astronomy was only one area of Digges’s mathematical work. He was also active in a range of other subjects, from navigation and surveying, to artillery and military science.2 Yet the diverse accounts of his mathematical work add up rather to a disparate resumé than to a coherent identification of Digges himself. There is currently no adequate answer to the simple question ‘Who was Thomas Digges?’. In part, this absence is due to a long-standing failure to distinguish clearly between the work of Thomas Digges and that of his father, Leonard (c.1520-c.1559); Thomas’s printed work was (quite literally) bound up with his father’s.3
Leonard had published two vernacular texts on mathematics in his lifetime: an almanac and prognostication which appeared under various titles throughout the century (first printed c.1555), and Tectonicon (1556), a text on mensuration and mathematical instruments. In addition to these published texts, Leonard promised a number of other works whose appearance was prevented by his early death. Some of this material was later prepared for posthumous publication by Thomas, who invariably made fresh additions of his own.
Thomas’s first publication is usually cited as Pantometria (1571). But this text on surveying and mensuration had been written by Leonard. Thomas explicitly stated that his own contribution was merely that of an editor, providing some clarification and emendation but leaving the substance of the work unchanged (1571: [page 52:] +2r-v).4 However, appended to Pantometria was a Mathematical Discourse of Geometrical Solids, a study of Platonic and Archimedean bodies which was clearly marked out as Thomas’s own. Thomas’s next publication, Alae seu scalae mathematicae (1573), a Latin text prompted by the new star of 1572, was unusual in being solely his responsibility. But Thomas returned to the role of literary executor in 1576 when he re-edited his father’s Prognostication Everlasting and added not only the Copernican Perfit Description of the Celestiall Orbes, but also brief discourses on navigation and magnetism. His last major new text was Stratioticos (1579), advertised on its title page as ‘An Arithmeticall Militare Treatise’. Stratioticos was written in three books, of which the first was based on a surviving draft of Leonard’s (1579: a2r). Although Thomas promised a number of other volumes none appeared in print; his only substantial further publications were slightly expanded second editions of Stratioticos (1590) and Pantometria (1591).5
This quick bibliographic review indicates how deeply interconnected were the published works of Leonard and Thomas Digges. It also suggests the difficulty of extricating the identities of father and son.6 The brief and cheap vernacular texts published by Leonard in the 1550s, with their emphasis on popular and practical mathematics, readily permit his identification as one of the earliest English [page 53:] mathematical practitioners. But what of his son? Thomas was certainly allotted a place in E.G.R. Taylor’s biographical listing of practitioners, but Taylor was ambivalent about Digges: she was suspicious of him, seeing him not as an admirably humble soul like Robert Norman or William Bourne but as an imperious (if not indeed arrogant) critic who was too ready to dismiss the efforts of ‘mere’ mechanicians.7
The uneasy feeling of personal disapproval underlying Taylor’s response to Digges might tempt us to disregard her comments. But we should not do so, because her reservations sprang from a limited reading of what is nevertheless genuine evidence. Fully incorporating that evidence into an account of Digges enables us to explain his actions and opinions rather than just judging them. So in this chapter, I will offer a new interpretation of the career of Thomas Digges. Rather than assuming that he was somehow born to the role of mathematical practitioner, I will show how he worked and reworked his role over a period of years. In particular, I will argue that his early ambitions and achievements cannot be readily reconciled with the now familiar vision of the mathematical practitioner, and that it was only in later years that he fashioned an identity which marks him out more closely as a practitioner.
Digges is an ideal figure for a study of changing mathematical identity, for he displayed a rare degree of self-consciousness when presenting himself and his works in the public medium of print. The sense that he was actively fashioning his own identity is most strikingly evident in Stratioticos (1579). In both the dedication and the preface to this military text, Digges looked back over the 1570s and claimed [page 54:] that he had switched from early contemplative concerns with mathematical demonstration to a new emphasis on practical actions in service of prince and country (1579: A2r, A3r-v).
Now, we should not necessarily take Digges’s polar opposition between current action and previous contemplation at face value; the very familiarity of the trope of action and contemplation should warn us that we are witnesses to rhetorical display rather than direct self-revelation. Indeed, when we come to look at the full range of Digges’s mathematics, the inadequacy of his language of action and contemplation becomes evident. The connotations of ‘contemplation’ seem inappropriate for the energetic and extensive work required by Digges’s early investigations of solid geometry and astronomy. Conversely, the detailed demonstrative exposition of artillery that Digges planned at the end of his life cannot be neatly reconciled within the category of ‘action’. So, in addition to the change he was eager to proclaim in 1579, there were thus also significant continuities throughout his career. Any adequate interpretation needs to both capture the character of his detailed mathematical work and yet at the same time accommodate Digges’s rhetoric, accounting for its language rather than either implicitly endorsing or explicitly rejecting it.
Digges’s autobiographical comments in Stratioticos also point us in another direction, towards his social rather than just his mathematical identity. Digges’s 1579 military discourse was topically dedicated to the Earl of Leicester, the prospective leader of an expeditionary force to the Netherlands against the Spanish. The more forcefully Digges emphasised the split between his previous and current selves, the more fully he was able to realign himself with the political, religious and military [page 55:] ethos of his patron and dedicatee.
We can thus place Digges’s reconstruction of identity within the contemporary operation of patronage. But we need a nuanced conception of patronage which treats it primarily as a medium of social credit rather than just a mechanism for the transfer of economic benefits from the elite to their social inferiors.8 Unfortunately, attempts to explain Digges’s career by reference to patronage have typically been conducted in reductionist terms. For example, through their economic ability to distribute largesse, Feingold depicts patrons as uniquely powerful in their influence over clients. He baldly states that ‘Thomas Digges virtually abandoned his theoretical studies once he entered the service of the Earl of Leicester’ and concludes that, in doing so, Digges was responding to his patron’s wishes.9 It is as if Digges was merely putty in the hands of his social superiors, unable to exert any personal choice.
Such accounts are theoretically flawed in their oversimplification of the character of patronage and also empirically inadequate for the specific case of Digges. For Digges had, in principle, considerable freedom to determine his own actions and allegiances. He was not dependent on the goodwill of patrons to secure a living, but could rely on his own resources: Digges was a substantial gentleman of independent [page 56:] means. Here we finally move towards the wider sense of Digges’s social identity. I shall argue that this expanded frame of reference is crucial for the interpretation of Digges’s changing role: to understand Digges as a mathematician means understanding him as a gentleman.
The Digges family was long-established in Kent. Though not at the very pinnacle of the county hierarchy, they were prominent figures, with extensive estates.10 Technically, Thomas Digges (and Leonard too) were not just gentlemen but, more correctly, esquires; all Thomas’s major publications contain woodcuts displaying the Diggeses’ coat of arms (Figure 2.1). However, the family’s status had been abruptly though temporarily overthrown in the 1550s during the Catholic reign of Mary, when Leonard was attainted of treason for his participation in the unsuccessful Wyatt rebellion. His death sentence was commuted and his confiscated lands and goods eventually returned on payment of fines.11 This family crisis must have sharpened the youthful Thomas’s sense of social status and privilege; fortunately for his future, both he and his younger brother were restored in blood by act of parliament in 1563, and were thus able to inherit Leonard’s property.12
Beyond the biographical meaning of his gentility, Thomas’s status had important implications for his career as a mathematician. Digges defined his early [page 57: Figure 2.1] [page 58:] identity as a mathematician through a link between the ‘nobility’ of social status and the intellectual nobility of subject matter and method. Later in his career, he realised himself as both a mathematician and gentleman through an ethic of civic service. This shift is crucial. For, while developing an explicit rhetoric of utility for prince and country, Digges was simultaneously working out a role for himself as a mathematical practitioner. By transforming his identity as a gentleman, Digges redefined the values towards which his mathematical activity was oriented.
The relationship between gentility and learning has recently been the subject of active research, focused particularly on 17th century natural philosophy.13 Examining the case of Digges gives a complementary insight into the constitution of mathematical identities in the 16th century. Digges’s reevaluation of his mathematical priorities was based on a shift between two different models of gentility: the first with the gentleman as intellectually and socially elite, the second identifying the gentleman as an active citizen. In Digges’s career, these are not mutually exclusive sets of values, one of which simply replaces the other. Rather they coexisted and regulated different areas of his life. It was the reinterpretation of mathematics as a subject most appropriately pursued by the active citizen that led to Digges’s new profession of faith in 1579. In this chapter I examine both Digges’s publications and his active service in order to understand his identities as both mathematician and gentleman.
2. POLYHEDRA, ASTRONOMY AND DIGGES’S EARLY CAREER
Between 1571 and 1576 Thomas Digges published three texts which shed [page 59:] valuable light on his early career and mathematical values. These three texts - the Mathematical Discourse (which accompanied Leonard Digges’s Pantometria), Alae seu scalae mathematicae, and the expanded edition of Leonard’s Prognostication Everlasting - provide the foundation for this section. Yet I want to begin not with Digges’s mathematical texts, but with the social relationships of this early period in his career.
Patronage provides a convenient point of entry. All three texts were dedicated to eminent patrons but in only one case do we have any further evidence of the patron-client relationship. Pantometria and the Mathematical Discourse (1571) were dedicated to Sir Nicholas Bacon, but Digges emphasised that this choice was a token rather of his father’s relationship with Bacon than his own. Similarly, the new edition of the Prognostication Everlasting was dedicated to the Lord High Admiral (Sir Edward Fiennes) because he had been Leonard’s earlier dedicatee for the text.
It is only with Alae seu scalae mathematicae (1573) that we have unequivocal evidence of a patronage relationship into which Thomas genuinely entered. Digges’s slim Latin treatise demonstrated such mathematical and instrumental techniques as he deemed necessary to determine the position and possible parallax of comets and celestial objects. It was occasioned by his efforts to study the ‘new star’ of 1572, a phenomenon which astounded Europe and became the subject of an outpouring of astronomical and astrological work.14 Digges’s contribution contained his determination of the nova’s fixed position along with his conclusion that it was indeed an authentically celestial phenomenon, whose appearance challenged the [page 60:] adequacy of traditional cosmology.
Alae was dedicated to Sir William Cecil, formerly Principal Secretary and now Lord Treasurer, who had recently been rewarded with that most rare of Elizabethan prizes, elevation to the nobility: he was created first Baron Burghley in 1572. Burghley was the political and administrative mainstay of Elizabeth’s reign and was one of the key figures in its system of personal and political advancement. Known as a man of learning, he was an apt target for the aspirations of any author seeking patronage and favour.
In the dedication to Alae, Digges attributed his astronomical efforts on the star to Burghley’s instigation. That this was more than the flattery typical of the genre is witnessed by a surviving letter from Digges to Burghley. The letter of December 1572 shows that Burghley had indeed been seeking Digges’s advice on the new phenomenon. However, Burghley’s concern was not with the mathematical determination of place, distance, and magnitude that was to engage Digges in Alae. Rather, Burghley wanted to find out the astrological meaning of this exceptional event. In response, Digges had
waded as far as ancient grounds of astrology and authors’ precepts of approved credit will bear me, to sift out the unknown influence of this new star or comet.15
Digges’s detailed conclusions were recorded in a seven point memorandum (now unfortunately lost) which originally accompanied his letter. The covering note does however make it clear that Digges provided Burghley only with general guidance on the terrestrial significance of the new phenomenon. The personal significance of the [page 61:] celestial apparition could only be gathered from an examination of individuals’ nativities.
A further letter from 1574 demonstrates that, after the publication of Alae, Digges remained a client of Burghley. As with the new star, we have only a covering note and not the text to which it acted as an enclosure.16 But, brief as it is, this second surviving letter reveals a great deal about the basis of Digges’s relationship with Burghley.
Digges begins by referring to his patron’s ‘Frame Astronomical’, by which must be meant the celestial ceiling structure installed in Burghley’s newly-built house, Theobalds.17 Digges may in fact have contributed to the design of this complex ‘frame’. It contained depictions of the northern constellations, each adorned with the appropriate number of stars, as well as a representation of the sun’s motion in the ecliptic performed by means of a hidden mechanism. Such a structure would have required the advice of someone with at least a modest amount of astronomical knowledge. Having already publicly demonstrated his astronomical prowess as a client of Burghley, Digges may well have initiated or been called on to assist in this piece of learned and ingenious architectural decoration.
But the principal purpose of Digges’s letter was to present Burghley with an [page 62:] astronomical treatise which would complement the new ‘Frame Astronomical’. The lost treatise included tables to determine the positions of stars in relation to the horizon, meridian, sun, and moon.
Whereupon sundry conclusions both pleasant for variety of knowledge and necessary for common use are grounded. Whereof I have in 50 conclusions digested the greater part, with their Histories Poetical and Judgements Astronomical.
But Digges did not just offer textual pleasure and utility, even if spiced by the poets’ accounts of the origins of the constellations.18 He also reported that he had found a workman able to execute a design for a polyhedral sundial which could be ‘placed in some of your Lordship’s gardens; as aptly serving for uses diurnal, as that other frame for conclusions done by night’. Clearly, Digges was offering Burghley ornamental constructions which were intended for conspicuous and impressive display.19
The exclusively mathematical content of Digges’s interaction with Burghley contrasts strikingly with the only other evidence from these early years of his career. In 1572, Digges entered parliament as M.P. for Wallingford. The exact circumstances of his selection are no longer recoverable, but self-consciously virtuous and able young gentlemen were increasingly making a name for themselves through parliamentary activity at this time.20 The House of Commons sat irregularly and [page 63:] infrequently and though much of its business was private and parochial, Digges immediately began to intervene in affairs of national importance: amongst other activity during his first session, he prepared a fierce memorandum calling for the execution of the Duke of Norfolk.21
What is the connection between the public world of parliament at Westminster and the private mathematical consultations that Burghley had with Digges? We seem to be in two different worlds, with Digges’s identity as a gentleman in parliament quite distinct from his identity as a mathematician. I suggest that Digges was indeed very deliberately creating separate identities for himself in these early years. But the evidence of a few surviving letters and a parliamentary memorandum is a slight basis for a compelling image of Digges’s early career. We need to turn to his texts.
The remainder of this section focuses further on Digges’s identity as a mathematician. I study Digges’s published work on solid geometry and astronomy, and reinforce the tentative conclusions that emerge from my examination of his patronage relationships and political activity. In his relations with Burghley in the early 1570s, the conjunction of astrological advice, poetic accomplishment and ingenious and prestigious devices suggests that Digges cannot be comfortably identified as a mathematical practitioner. Indeed, the Burghley evidence might tempt [page 64:] us to identify Digges’s role as closer to that of a courtly mathematicus. However, the primary significance of Digges’s texts is less in providing us with a recognisable and familiar social role, and more in presenting mathematics as a world unto itself, distinct from the base concerns of ordinary mortals.
In emphasising the descriptive inadequacy of the role of the practitioner for this early stage in Digges’s career, there is one initial obstacle to be overcome: how do we explain his edition of Pantometria? This text was billed as a ‘geometrical practise’ and dealt with the instruments and procedures of surveying and mensuration, the calculation of areas and the determination of volumes (Figure 2.2). Pantometria thus falls squarely within the canon of mathematical practice. Does Thomas’s edition of his father’s text mean that he was endorsing the role of the practitioner? I suggest that, while quite willing to accept and promote his father’s work, Thomas rated it lower on his scale of priorities than his own more advanced studies of geometrical solids.
The disparity between Leonard’s Pantometria and Thomas’s Mathematical Discourse is evident from their respective apologia in the general preface to the whole volume. Thomas presents the primary virtues of Pantometria as utility and pleasure. When it comes to the defence of the Mathematical Discourse, he adopts a different and more robust strategy, targeting his text at readers ‘desiring the knowledge of things somewhat passing the reach and capacity of the common sort’ (1571: A4r). In his rhetorical stance it was not utility but intellectual elevation that served as the highest end. Digges therefore feigned to ignore those who might castigate his advanced study of polyhedra as ‘a fond toy, a mere curious trifle, serving to no use or commodity’. Unless a detractor genuinely valued the study of ‘hard and difficult’ [page 65: Figure 2.2] [page 66:] matters, persuasion would be useless. Digges rounded on potential critics as ‘two-footed moles and toads whom destiny and nature hath ordained to crawl within the earth, and suck upon the muck’; such men ‘may not possibly by any vehement exhortation be reduced or moved to taste or savour any whit of virtue, science, or any such celestial influence’ (1571: A4r).
Where did this leave the mathematician? Not in the realm of lucre and worldly pleasure but placed on high in the company of geometers such as Euclid, Archimedes, and Apollonius. Digges’s forceful language and stark division of men into either virtuous mathematicians or ignorant followers of Epicurus and Midas took him well away from the mathematician’s role implicit in Pantometria. His faith in the intrinsic worth of advanced studies led him to emphasise his solid geometry as a pacific discipline little adapted to either military or civic necessities. His Discourse therefore embodied mathematics not as a worldly vocational pursuit but as the work of a gentleman who primarily prized intellectual nobility.
It is one thing to decipher the high-flown rhetoric surrounding Digges’s presentation of his Mathematical Discourse, but something else to show that the content of the treatise conforms to the values that Digges espoused. We need to check whether content matches rhetoric.
The Mathematical Discourse is primarily concerned with the properties, dimensions, and interrelations of the five regular (Platonic) solids (Figure 2.3). Its text gives several hundred theorems dealing with such topics as the mutual inscription and circumscription of these solids. The final section of the text investigates similar questions but does so by studying five ‘transformed’ bodies - semi-regular [page 67: Figure 2.3] [page 68:] Archimedean solids generated by the metamorphosis of each of the five Platonic solids. The Mathematical Discourse covers its subject in just over one hundred pages, but its brevity is deceptive. The amount of labour invested in its preparation is disguised by Digges’s decision to omit proofs of his mass of theorems. His reason was brevity (1571: Aa1r); certainly, if demonstrations had been supplied, the bulk of the text would have been multiplied many times over.
The principal point of reference (and the only text actually cited by Digges) was Euclid’s Elements. Aligning Digges’s Mathematical Discourse with the Elements may leave the modern reader with an initial feeling of disappointment. Is this really a likely site for advanced and elevated work? The Elements is now apt to evoke the sense of a complete and well-established work, a classical monument, perfect but perhaps sterile. However, for Digges and his contemporaries it was far from being a dead text; on the contrary, it was a site for active work and debate. There were many minor points of interpretation and emendation, but also areas of major controversy extending as far as questions of authorship.22 Even the size of the work differed from that of modern editions: in addition to the 13 books now attributed to Euclid, there were two further books on solid geometry in 16th-century editions.23
It was from what are now considered the spurious books XIV and XV that Digges principally took his cue. These additional books consider the inscription of some of the regular solids in a sphere and also within each other.24 However, the presentation is not complete and subsequent authors in the Euclidean tradition [page 69:] attempted to improve and systematise. For example, Campanus of Novara’s 13th-century edition added seven new inscriptions to the five given in book XV, while Piero della Francesca not only devised a further inscription but provided new alternatives to two of those given by Campanus.25 These attempts to go beyond the results in the Greek text reached their apotheosis with the editions of Euclid published by a French contemporary of Digges, François Foix de Candalle (Flussas). In his 1566 edition, Candalle added a new book XVI and gave the theoretical maximum of 20 mutual inscriptions of the regular solids. (His second edition of the Elements of 1578 was expanded to 18 books!) Moreover, his work was available in England, since it was incorporated in translation in Billingsley’s 1570 English Euclid.
Digges responded independently to this tradition, providing many new results on the proportions of mutually inscribed and circumscribed bodies. Moreover, he stated that not all 20 possible inscriptions were actually feasible, implicitly reproving the (over)enthusiasm of Candalle (1571: Bb2r, Bb3v, Cc1v).
This independence of approach was matched in the account of his ‘transformed’ (Archimedean) bodies. On the title page of the volume, Digges described these as ‘five other equilater uniform solids geometrical, of his own invention, hitherto not mentioned of by any geometricians’. All thirteen of the semi-regular solids had actually been known to Archimedes, so Digges was not accurate in his claim that these bodies were newly discovered by himself.26 But only a few 16th [page 70:] century texts discussed or illustrated any of the Archimedean solids.27 It seems probable that Digges sincerely believed himself to be offering a substantial new contribution. One probably familiar source - Candalle (whether in the Latin edition of 1566 or as incorporated into English in 1570) - had indeed provided a discourse on two ‘new’ (actually Archimedean) solids. But these two polyhedra were not mentioned by Digges, who dealt only with his own five solids (see Figure 2.4 for examples).
Even in his style of presentation, Digges displayed his independence and was not bound by the established format of the geometrical genre. Rather than following the Euclidean example of painstakingly demonstrated constructions and theorems, Digges proceeded ‘geometrically by algebraical calculations’ (1571: S4v). He concentrated on the algebraic task of deriving numerical values for unknown magnitudes of solids and spheres, whether lengths, areas or volumes. The combination of geometric diagram (though not formal geometric construction) with algebraic working gives Digges’s treatise a distinctive appearance (Figure 2.5).
I emphasise the independence and novelty of Digges’s Mathematical Discourse not for purposes of celebration, but because Digges proudly proclaimed that his text treated of matters ‘new, rare and difficult’ (1571: S4v). As a mathematician, Digges aspired ‘to reach above the common sort’ (ibid.), and his intellectual elitism was mirrored in the values which he ascribed to the regular solids and their study. For Digges, the Platonic bodies were the embodiment of nobility and purity. They symbolised an order beyond the mundane realm of mutability and decay, and could [page 71: Figure 2.4] [page 72: Figure 2.5] [page 73:] not fail to inspire pleasure and delight, at least in a mind that was suitably ‘noble, free, or well disposed’ (1571: +2v). The intellectual, moral and social independence of the gentleman was here effectively written into Digges’s standards for the mathematician. With that freedom assumed, the study of polyhedra could become its own reward. And so, what higher achievement could a mathematician aim for than the extension of this independent domain of order, beauty, and regularity? By his ‘discovery’ of new solids which ‘seem only to lose the form and yet still retain the nature’ of the regular solids (1571: Ff4v), Digges was enlarging the dominion of that form of mathematical reason which he held in highest esteem.
Digges considered that nothing should be allowed to sully the purity of high geometry. Not just vulgar concerns with utility and profit were excluded by this prescription. Digges would not even allow any philosophical ‘pollution’ of the certain and self-sufficient domain of mathematics. In the preface to his treatise Digges notes that he will not
discourse of [the regular solids’] secret or mystical appliances to the elemental regions and frame of the celestial spheres, as things remote and far distant from the method, nature and certainty of geometrical demonstration (1571: S4v).
The most obvious object of this implied reproach was the Platonic theory of the elements, as expounded in Timaeus. But Digges may have had a much more contemporary target in mind: Offusius’s De divina astrorum facultate (1570), in which the regular solids were used to determine cosmic and elemental proportions.28 Evidently Digges meant not to meddle with such uncertain matters as natural or astrological philosophy. Yet whoever Digges meant to censure, his comments serve [page 74:] chiefly to highlight his contrasting image of geometry and his distinct identity as a mathematician.
Digges promised that if these first mathematical fruits of his studies were liked and accepted, he would produce a sequel to contain not only the demonstrations of his theorems but also a further extension to introduce results based on conic sections, and on solids generated by their revolution (1571: A4r-v, S4v-T1r). We can only presume that the Mathematical Discourse was met by (at best) a deafening silence, for no such additional volume appeared. Likewise, historians have given the work almost no notice. By contrast, Digges’s astronomy, though unevenly studied, has at least figured more prominently in the literature.
Digges’s astronomical work needs to be approached with some care, for it appears in two very different texts, Alae seu scalae mathematicae (1573) and the Perfit Description (1576). Alae is in Latin, the Perfit Description in the vernacular; Alae is significant for European astronomy, the Perfit Description for English Copernicanism; Alae displays its learning and status through the format of mathematical demonstration, while the discursive form of the Perfit Description was meant for inclusion in a cheap and already popular volume. Interpretations which ignore the highly specific character of each of the two texts almost inevitably go awry, especially if they reduce Digges’s astronomy to only the Perfit Description, and then forget that it was knowingly written for the well-established populist genre of prognostications and almanacs.29
Nevertheless, with all these caveats assumed, I will draw on both of Digges’s [page 75:] texts in order to examine his astronomy. As with his solid geometry, I will sketch his rhetorical presentation of astronomy and the identity of the mathematician, while also investigating the match between rhetoric and content. Again, as with the regular polyhedra, part of the justification for astronomy was that its objects were inherently ennobling and worthy of study. However, the literature of astronomy offered a far richer stream of linguistic resources within which to order one’s identity and activity. Through familiar metaphor and newly reshaped religious doctrine, mathematical astronomy was for Digges a profoundly moral enterprise.
Of fundamental importance was the contrast between the celestial and sublunary realms; this marks a divide along which Digges aligned a host of further dichotomies.30 In both Alae seu scalae mathematicae and the Perfect Description he contrasted the perfection and regularity of the heavens with the terrestrial world of generation and corruption. Above, there is the immutable empire of uniform, eternal, and pure substance. The heavens are the sacred temple for the Calvinist elect, while mortal sinners live out their days on the dark star of the earth. Resplendent with beauty, the celestial spheres attract the mind upwards away from the dregs of the body and entice noble reason with the prospect of joy and felicity, removed from all worldly troubles. All that is blessed finds its true home above, while mutability and decay are the destiny of the profane beings who dwell here below. Celestial order, simplicity, and harmony are opposed to sublunary irregularity and the uncertain, base, and foul cares of humanity.31 [page 76:]
Now, Digges was not alone in passionately valuing celestial order; as many historians have remarked, this is a constant of Elizabethan culture.32 But Digges’s sense of order did not simply bolster the status quo of the traditional world picture, as it did for his contemporaries. So how did Digges come to espouse a Copernican rather than a traditional cosmology? The answer lies in his extraordinary elevation of mathematics.
Beyond the realm of a few principles - such as the simplicity and order of the heavens - which he takes as axiomatic, Digges considered that specifically mathematical techniques of investigation and argument were the best available for the domain of astronomy. Mathematics was not just a tool to save the phenomena but the means to arrive at the truth. Indeed, Digges considered that Copernicus’s great achievement had been to restore the perfect anatomy of the heavens as an interconnected planetary system, and he repeatedly echoed Copernicus’s condemnation of the ‘monstrous’, botched arrangement of the Ptolemaic spheres (1573: A4v, 2A3r, 2A4v, L2v).
If mathematics was able to demonstratively restore the perfect order of the celestial spheres, what role was allotted to philosophy, traditionally placed above mathematics in disciplinary hierarchies? Digges considered that, in contrast to the demonstrative certainty of mathematics, philosophy could offer only plausible or [page 77:] probable arguments.33 This relative evaluation of mathematics and philosophy helps to explain the structure and sequence of the Perfit Description. Digges inverted the order of presentation in Copernicus’s De Revolutionibus and began his adapted translation with I, 10: ‘On the order of the celestial spheres’. Here Copernicus had presented his new arrangement of the planets and given a mathematical justification for his scheme. Only after reading this principal (and, for Digges, self-sufficient) argument are we then taken back to De Revolutionibus I, 7-9 where Copernicus had stated and then disputed the standard philosophical reasons against the motion of the earth. Digges made his expository strategy quite clear:
because the world hath so long a time been carried with an opinion of the earth’s stability, as the contrary cannot now be very impersuasible, I have thought good out of Copernicus also to give a taste of the reasons philosophical alleged for the earth’s stability, and their solutions, [so] that such as are not able with geometrical eyes to behold the secret perfection of Copernicus’s Theoric may yet by these familiar, natural reasons be induced to search further, and not rashly to condemn for fantastical so ancient doctrine revived and by Copernicus so demonstratively approved (1576: N4r).
The realm of philosophy is only for those who lack ‘geometrical eyes’ and remain stuck with probable argument and the deceptive evidence of the senses. However, while Digges frequently vaunted (mathematical) reason at the expense of the senses (eg 1576: M1v), in Alae seu scalae mathematicae he nevertheless acknowledged that the proper practice of astronomy depended on two complementary components: sensible experience as well as mathematical demonstration (1573: H4r). It is therefore to Alae that we should look for Digges’s detailed translation of [page 78:] mathematical rhetoric into a programme of astronomical work.
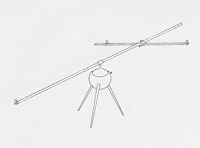
When Digges first began to observe the new star he searched his astronomical texts for techniques to accurately determine its position. Since the new body neither looked like nor seemed to move like a comet, the most significant problem quickly became that of finding out whether it was above or below the sphere of the moon. Determining the object’s parallax was the only available method and a short treatise by Regiomontanus offered the best technique for carrying out the task.34 However, Digges discovered that although Regiomontanus’s method was irrefutably accurate in principle it frequently led to errors in practice. These errors were the cumulative result of the large number of observations which the method required. In observations of objects close to the earth, as Digges supposed comets to be, the combination of slight inaccuracies would scarcely affect the parallax of the observed body. But in the case of the new star the parallax was extremely small - no more than two minutes - and possibly even altogether insensible. Accumulated observational errors of the sort that afflicted Regiomontanus’s technique would completely swamp the parallax for which Digges was looking. Digges’s rejection of Regiomontanus’s method as insufficiently adapted to practice was diplomatic but firm.35 Reason might be enthroned as ‘Regina Ratio’, but she should not prescribe laws which the dull and undiscerning senses were incapable of following (1573: 2A3v, H4r).
Thus the first half of Alae is given over to a demonstrative sequence of trigonometrical theorems on parallax. Digges elaborated several different procedures, [page 79:] hoping to construct a reliable method to minimise the difficulties that bedeviled Regiomontanus’s approach. He particularly wanted to find a method adapted to his favoured instrument, the radius astronomicus. Digges had selected the radius after reviewing the instrumental armoury of astronomy and finding nothing that could surpass it for ease of handling or ability to discern extremely small angular intervals (1573: H4r). Yet existing treatments of the instrument contained various inadequacies and Digges successfully set out to rectify all of its systematic sources of error. The resulting instrument, with its 10 foot brass main staff, had a distinctive hollow triangular cross section (for lightness) and an added pinnule at the observing end to banish the problem of the eye’s eccentricity (Figure 2.6).36 Moreover both the main staff and transversary were decimally graduated and their accuracy greatly enhanced by the use of transversal divisions (Figure 2.7).37 Digges’s scrupulous concern for accuracy had two results: firstly, he established that the phenomenon was celestial; secondly, he achieved a precise placing of the new star in relation to the surrounding stars of Cassiopeia. In his Progymnasta (1602), Tycho retrospectively ranked Digges’s observations second only to his own; however, recent radio astronomical work on the remnant of the new star has shown that it was Tycho’s rather than Digges’s observations which displayed systematic error. Digges was spot on.38
As with Digges’s polyhedral inventions, my concern in highlighting his astronomical successes is not simply to glorify his name. The point is that Digges did [page 80: Figure 2.6] [page 81: Figure 2.7] [page 82:] not just remain within the rhetoric of elevated and advanced study. To redeem his promises and uphold his pronouncements he immersed himself in the highly detailed labour of trigonometrical innovation and instrumental rectification. To construct irrefutable demonstrations, to seek observational precision, and to extirpate error required active intervention and work, rather than just armchair prose.
On the title page of his own copy of Copernicus, Digges inscribed a simple but telling tag: ‘Vulgi opinio error’.39 For Digges, the common sort remained stuck in the ignorance of erroneous opinion, while the noble mathematician could fly upwards to rare and difficult realms (using either the mathematical wings or the more pedestrian - but punning - ladders or scales in the title of Alae). The metaphors of ascent and isolation from the common crowd were part of a well-established language justifying the location and practice of advanced study. But, though well-worn, these tropes were still powerful. Digges’s brief tag encapsulated what he set himself against in his pursuit of astronomy and, by contrast, highlighted what he valued in its study. He sought to differentiate himself from, and reach above, the common sort. He sought not mere opinion but the demonstrative knowledge that could be secured only through the mathematical sciences. Finally, he sought to correct error, no matter how authoritative or long-established, and to replace it with the truth of mathematical reason and rigidly disciplined experience.
In Digges’s early work, the link between gentleman and mathematician was through the idea of nobility. The mathematical gentleman should study noble topics which correspond with his high status. Nobility should attach not just to the body of [page 83:] the gentleman but also to the mind. By their subject matter, by their demonstrative certainty, by their distance from the vulgar preoccupations of the world, Digges characterised geometry and astronomy as subjects peculiarly appropriate for a liberal mind (1573: A4r). Digges published the Perfect Description so that ‘such noble English minds (as delight to reach above the baser sort of men) might not be altogether defrauded of so noble a part of Philosophy’.40 Digges’s reference to the ‘baser sort of men’ indicates his close linking of intellectual and social nobility (or gentility). Those who are common and vulgar can never expect to comprehend or appreciate the efforts and results of the elevated mathematician. Novelty and difficulty, rather than being signs of vanity or false pride, were for Digges almost guarantees of moral rectitude, for they carried him beyond the concerns of the common sort.
Digges did not try to square his identity as a mathematician with his membership of parliament. As an MP, he acted as a gentleman within contemporary English society. But as a mathematician, Digges appealed to different gentle values and deliberately distanced his mathematics from the concerns that he expressed as a youthful and energetic newcomer to the House of Commons. The point is not that mathematics was ‘essentially’ otherworldly, rather that he had to make it that way. In doing so he carved out a mathematical identity which cannot be readily reconciled with that typical of the mathematical practitioner. [page 84:]
3. THE ACTIVE CITIZEN
After showing how difficult it is to pigeonhole the youthful Digges as a mathematical practitioner, I now want to display and interpret the reformed commitments of his later career. Digges himself invites us to see sweeping change. When writing Stratioticos in late 1579 he offered an autobiographical story of discontinuity: reflecting on his work of the early 1570s, he confessed that
the strange variety of inventions in the more subtle part of these mathematical demonstrations did breed in me for a time a singular delectation (1579: A3r).
But this pleasure had not been sustained. Digges’s readers were now shown a different image of his work as a mathematician. With maturer judgement, Digges had turned from subtlety and delight to practicality and utility. He stated that he had latterly
spent many of my years in reducing the Sciences Mathematical from Demonstrative Contemplations to Experimental Actions, for the Service of my Prince and Country (1579: A2r).
Following Digges’s own lead, I shall argue that in his later career Digges’s primary aspiration was to realise himself as an active servant of the Protestant commonwealth. But despite following Digges’s own emphasis on service, I will not rely on his language of contemplation and action as the explanation of his shifting commitments. Rather, my account dwells on his roles as a gentleman. We have already seen Digges performing two different gentlemanly roles, one which depended on the nobility and independence of the mind as a guarantor of social nobility, the other enacted through the civic virtue of parliamentary activity. My argument here is that, in his later career, Digges shifted his role as a mathematician from the first to the second of these gentlemanly ideals. Although once elevated as reason’s noble and [page 85:] independent effort to uncover truth, mathematics was now to be praised firstly for its practical and particularly military merits.
Digges did not abandon his intellectual allegiance to mathematical matters high and difficult, but he subordinated these values to the virtues of service to prince, country, and (Protestant) ‘true religion’. In transferring his identity as a mathematician from one ideal of gentlemanly conduct to another, Digges cast a role for himself that is recognisably closer to that of a mathematical practitioner. Digges’s reformulation and proclamation of his new role thus marks a significant moment in the public fortunes of the mathematical arts.
In tracing Digges’s development as an active citizen, the place to begin is the House of Commons. We have already seen that Digges was selected as a member of parliament for Wallingford in 1572. The Parliament of 1572 had further sessions in 1576 and 1581 and was dissolved only in 1583. Digges was then returned as a member for Southampton when a new parliament was called in 1584. The twin session over the winter of 1584-5 was the only sitting before dissolution in 1586. Between 1572 and 1586 there were thus five sessions of the House of Commons, covering a total of about 8 months of actual sittings.41 Compared to the modern parliament, membership was an infrequent and irregular duty. Yet I suggest that parliament gives us access to Digges’s political education and his assumption of increasingly heavy responsibilities and authority. As long as we do not put too heavy an explanatory burden on his membership, Digges’s experience of parliament acts as a convenient pointer to his changing identity and priorities. [page 86:]
In the later 16th and early 17th centuries, parliament was increasingly seen as a sort of finishing school for the sons of gentry. Younger members could learn the appropriate virtues of civic service from their elders in an environment with its own distinctive intellectual values. Mere scholarly disputation and ostentation of wit were to be shunned in favour of the mature consideration of weighty matters.42
Digges learnt his lesson well. He became a ‘man of business’, one of a small group who diligently served the Privy Council by bringing in motions and directing debate towards the conclusions desired by senior administrative figures such as Burghley (who by now was elevated to the Lords).43 By the 1580s, Digges was an authoritative figure; an anonymous diarist of the 1584 parliament noted that ‘Digges commonly doth speak last and therefore saith every matter must have an end and therefore to draw this to a conclusion.’44 Digges had emerged as a respected figure of some standing and authority, who busied himself drafting memoranda, working closely with the Privy Council, sitting on committees, and suggesting policy.45 Digges’s participation in the harbour works at Dover, arguing for their importance in terms of both economic development and national security, was closely linked to this [page 87:] parliamentary activity.46
Digges’s parliamentary work culminated in a whirlwind of papers which were prepared for the session of 1584-5. At the height of his powers and political influence, Digges wrote and circulated brief manuscript tracts on a whole range of interconnected topics: on the provision of a large standing army; against the Oath of Association; against a bill on Jesuits; and on the question of the Succession to Queen Elizabeth.47
Digges’s political and religious perceptions emerge clearly from these tracts. England is seen as an isolated and threatened island, standing out against the might of Spain.48 External danger is matched by the possibility of internal disturbance: the advent of the much-feared Jesuit missionaries in the 1580s led to renewed worries of Catholic insurgency. Such new developments took place against an already troubled background. Not only had the Pope excommunicated the Queen at the beginning of the 1570s but he had absolved English Catholics from their oath of allegiance to Elizabeth and encouraged them to seek her overthrow. Particularly after the 1584 assassination of William the Silent, Prince of Orange, Digges shared contemporary fears that the same fate might befall Elizabeth. Digges certainly recognised that no ordinary punishments could stop the ‘hellhound Jesuits’, who would willingly become martyrs to overthrow English Protestantism. Moreover, with no universally [page 88:] recognised heir, Elizabeth’s death (whether natural or not) could lead the country towards civil strife and thus disaster. A loyal standing army of 40,000 men was needed to suppress internal dissension and also to repulse any foreign invaders.
While primarily desiring to safeguard the commonwealth of England, Digges did not have a narrowly nationalistic outlook. He also promoted a more international conception of Protestantism in which England should support the Dutch in their struggle against the Spanish. In his foreign policy, Digges belonged to the activist and interventionist wing who focused their hopes and aspirations on the Earl of Leicester rather than the more cautious Lord Burghley.49
Leicester brings us back to Stratioticos, the text whose dedication he received in 1579. Stratioticos exemplifies the new connection that Digges was establishing between mathematics and active service. This ‘arithmetical military treatise’ begins with a short introductory book on basic arithmetic deriving from unpublished material of Leonard Digges (1579: a2r). The remaining two books are Thomas’s own. Book 2 deals with the elementary algebra of use to a soldier (together with a range of practical examples), while book 3 gives a lengthy treatment of the qualities and roles of all the ranks of men in an army. Finally there is some concluding material on the arrangement of troops in battle and in camp, as well as a sequence of questions on artillery.
The military emphasis of the text is very deliberate. Digges announced that ‘the Art and Profession only or chiefly convenient for the Nobility and Gentlemen of [page 89:] this land’ was to be ‘serviceable for the State in causes military’ (1579: 70). In addition to this new declaration of gentlemanly allegiance, there were more specific circumstances behind Digges’s choice of subject. Over the winter of 1577-8 it had seemed possible that the Earl of Leicester would lead an expedition against the Spanish in the Netherlands.50 For Digges, it was ‘the Fame of [this] honourable enterprise ... [that] did first move me to employ my Mathematical Muses upon this Military Argument’ (1579: A2v). The text of Stratioticos had been presented to Leicester in manuscript form as Digges’s response to the possibility of military intervention, and book 3 gave in effect a blueprint for Leicester’s army.
Although Leicester’s expedition came to nothing, a force of English mercenaries was sent to the Low Countries in the summer of 1578. Digges was himself there in the autumn and, while touring and reporting on fortifications, he witnessed and was appalled by the disorder of the troops.51 An insistent theme of Stratioticos thus became the need for military preparedness and discipline. Digges exhorted his countrymen ‘to awake our Nation out of that secure Dream’ fostered by the pacific reign of Elizabeth (1579: a1r). The absence of war had brought prosperity and stability to the realm but there were dangers accompanying this notable benefit. It was all too tempting to neglect military discipline while enjoying the fruits of peace. Digges drew not only on his own experience but extracted contemporary lessons from history, which [page 90:]
did plainly demonstrate unto me that the well and evil using of this military discipline among all natural causes was the greatest, or rather the only, occasion of the advancing, establishing, or razing and defacing of all Monarchies, Empires, Kingdoms and Commonweals (1579: A3v-4r).
Even the once invincible Roman Empire, whose military ordinances Digges studied, admired, and advocated, had eventually fallen into ruin and miserable servitude as a consequence of the corruption of military discipline. Digges’s historical reading reinforced the crucial importance of maintaining military order and discipline. He presented Stratioticos as ‘tending chiefly to this end that our Nation in this happy peace may not rest altogether careless of wars’ (1579: a1r-v).
Although the prospect of officially sanctioned military intervention in the Netherlands had receded at the end of the 1570s, it once more came to the fore in the mid-1580s. Leicester was still the figurehead for those favouring an activist and interventionist policy and was seen as the natural leader of an expeditionary force. Moreover, as Digges’s principal patron of the late 1570s and 1580s, and the nobleman whose political and religious stance he felt closest to, Digges both encouraged Leicester to action and sought his own reward through virtuous service.52 Writing to Leicester in June 1585 he enclosed some preliminary notes for ‘a plat of military ordinance for that army that I hope to see led under your honourable conduit’,
hoping your Lordship will vouchsafe to embrace and not to omit so honourable an occasion in purchasing the safety of her Majesty and your country, and relieving the oppressed Christians in those afflicted Provinces, to win yourself also fame immortal; wherein [page 91:] I hope your Lordship shall perceive I have not so vainly spent my life but I shall be able to do you some service.53
Digges’s petition for office in Leicester’s army did not fall on deaf ears. He was appointed as both trench master and muster master in the expeditionary force and, on arrival, immediately busied himself as a gentleman mathematical practitioner, surveying fortifications. However, after Leicester made his entry a month later (at the very end of 1585), Digges devoted himself wholly to the office of muster master, ‘which being so far out of frame required an entire man (not any other way employed) to take the care and charge thereof’.54
The transition from the prescriptions and model army of Stratioticos to the realities of the Netherlands campaign threw up enormous obstacles for Digges. As muster master, Digges was responsible for taking the rolls of the companies and ensuring that the correct amounts of pay were distributed to the captains (and thence to the men). It was an office Digges exercised with self-conscious rectitude and for which he won Leicester’s praise.55 Yet though Digges sought to stamp out corrupt financial practices, his efforts were hampered by his inability to guarantee the supply of money reaching him. While attempting to enforce proper procedures on company captains, he was unable to extract regular funding from his own superiors to pass on as paymaster. Not surprisingly, Digges faced increasing hostility. By September [page 92:] 1586 he confessed that the burden of malice against him had become intolerable.56 When he finally received his official discharge in early 1588 he considered that the disorders and abuses plaguing the army were above his power to remedy.57
The apparent chaos of the Netherlands campaign broke Digges’s health and he was eventually to despair of earthly redress and his full return to royal favour.58 Digges’s final and most committed venture in the role of the militarily active citizen had ended in disenchantment. Yet he did not lapse into cynicism or apathy. Digges defended Leicester in print from the slanderous insinuations in circulation against him.59 Even after Leicester’s death in 1588, Digges guarded the reputation and military honour of his erstwhile patron.60 Nor did Digges forsake the values which had led him to participate in the Netherlands expedition. Although wearied by the experience, he preserved his sense of righteous service to prince, country, and Protestantism. Writing to Burghley in 1590 he testified to his ‘duty and zeal to god, and the service of my sacred Sovereign which in me shall never be quenched’.61
Badly bruised as he may have been, Digges held fast to the role which he had defined for himself in the later 1570s. As a virtuous gentleman and military intellectual his ideals remained those of service. The second edition of Stratioticos [page 93:] (1590) enabled him to restate (and partly revise) his account of a model army and the attainments of its members. In his account of the general, the role to which he allots greatest space in book three of Stratioticos, Digges reveals those qualities which he most admired and sought to emulate.
For Digges, the ideal military leader must be the most learned, virtuous, experienced, and religious of men, in order to inspire the loyalty and trust of his subordinates. Most striking is Digges’s insistence on the two intellectual disciplines which can contribute most to the instruction and proper formation of the general: history and the mathematical arts.62 These had provided Digges with the foundation for Stratioticos itself. It was his reading of ancient histories which convinced Digges that military science and discipline were together ‘the Roof and outward covering to defend and guard [the Kingdom] from the wind and rain, and furious storms of foreign tempests’ (1579/1590: A2v). The mathematical arts offered a contemporary complement which could be put into direct execution. They could serve as a principal bulwark of military order and expert procedure, and further the reformation of otherwise corrupt discipline. Although he could never aspire to achieve the post of general himself, Digges’s description of the ideal commander encapsulates those qualities that he attempted to exemplify in his own career. Having seen how Digges shifted his early mathematical skills towards the support of his role as active citizen, we should now look more closely at his later efforts in the mathematical sciences.[page 94:]
4. ARTILLERY AS MATHEMATICAL SCIENCE
In the first edition of Stratioticos Digges listed his existing work in print and also set out a programme of mathematical publication (1579: a3v-a4v). Digges’s programme comprised six treatises that he wished to complete and bring to press. The planned volumes were to deal with navigation and magnetic variation, ‘architecture nautical’ (the mathematics of shipbuilding, cf. chapter 3 below), a commentary on Copernicus, sundials, artillery and pyrotechny, and fortification. Digges also promised elsewhere to deliver an advanced text on algebra as a supplement to the narrowly military account that he gave in book two of Stratioticos (1579: 32). None of these promised texts were ever to appear but the fragments and advance notices that Digges did publish allow us to investigate how he treated the mathematical arts in the latter part of his career.
Among the subjects which his programme highlighted, Copernican astronomy and dialling rapidly dropped from prominence. Together with algebra, they disappeared from Digges’s agenda during the 1580s; indeed, Digges had omitted to mention them in his 1579 dedication to Leicester which cited the other discourses that he had already begun (1579: A2r). Of those other topics, navigation remained a concern and is one of the best indicators of Digges’s changing mathematical values (see chapter 4 below). He also retained a commitment to the publication of his military discourses. In the second editions of Stratioticos (1590) and Pantometria (1591) Digges renewed his promises to publish on nautical architecture and fortification.
But of all the subjects with which Digges engaged, artillery emerged as of [page 95:] highest significance. Already in the first edition of Stratioticos he had explicitly singled it out as his first priority for research and publication (1579: 190-1). In that text he included a series of questions designed to encourage mathematicians and gunners to a closer examination of the art. Many of these questions were answered by marginal annotations in the second edition of 1590, to which Digges appended a further discourse dealing with various errors that had appeared in print. Not content with resolving his own questions and warning of other authors’ errors, he also included fresh material on artillery in the expanded reissue of Pantometria (1591).
By repeatedly returning to artillery, Digges endorsed its importance as an exemplary mathematical art. The military significance of artillery was evident to all, and Digges scarcely needed to argue for its value in the service of prince and country. It was altogether appropriate for ‘a gentleman that professeth the wars’. The prominence of artillery in Digges’s later career fits closely with the avowed values which his mathematics was claimed to support.
Moreover, Digges’s work on artillery was not just significant for his own career. The cumulative effect of his publications gave urgency to the investigation of great ordnance. As one of the first and most prominent English authors to analyse gunnery problems, Digges played a major role in establishing artillery as a specifically mathematical art.63
In publishing on artillery, Digges was once again taking up a topic that had been pursued by his father. Leonard Digges had studied Tartaglia and other [page 96:] mathematicians and, like them, he had attempted to provide an account of ballistic trajectories and a way of predicting ranges. But Leonard’s work was not confined to the study of texts: he undertook what was evidently a lengthy programme of self-consciously experimental investigation. This series of trials convinced him that even notable mathematicians such as Tartaglia had erred in the very first principles of the science. Leonard’s practical work provided him with a foundation from which to judge the worth of others’ efforts and he had promised a book in which he would deliver an adequate treatment of artillery as a mathematical art.64
Leonard’s book never reached the press but Thomas presumably had access to surviving manuscripts, for he was fulsome in his declaration of indebtedness (1591: 175-6). Thomas’s self-confessed reliance on his father’s work makes it difficult to distinguish his own results from those of Leonard. Only when Thomas makes a specific attribution can we be confident of who was responsible for an individual conclusion. Yet Thomas was certainly tackling the subject independently. Pantometria records Leonard’s belief that he had ‘at the last reduced that most irregular course and circuit of the bullet ... within the bounds of numbers and arithmetical rules’ (1571: I4r). Thomas was not so sanguine. In 1579 he admitted that
there are yet many mysteries that by further proofs and trials experimental I must resolve before I can reduce that art to such perfection as can content me (1579: 191).
Writing twelve years later he was still not satisfied that he had achieved a full and accurate understanding of the problems of artillery (1591: 56). Demanding a level of rigour appropriate to mathematical discourse, Digges appears to have held back his much-heralded treatise on artillery because he could not meet his own self-imposed [page 97:] standards: ‘the more a man knows the more he still learns his own wants’ (1590: 368).
Even if Digges was unable to furnish a polished and complete doctrine of his own, he could still correct the errors of others so ‘that practitioners in great artillery may use these notes as sea marks to escape the rocks’.65 But it is the fragmentary traces of his own positive conclusions that are most revealing of the aims and methods of his mathematical artillery.
Gunnery was a difficult, dangerous and highly expensive activity. In amongst the smoke, the noise, and the recoiling of the piece it was not immediately obvious how the mathematician could advance the gunner’s art.66 In Stratioticos (1579) Digges began with a sharp distinction between four principal ‘causes’ and all of the other factors which affected the performance of a piece. The secondary or accidental causes included the rarity or density of the air, the presence of wind, the wadding and ramming of the charge, the irregularity of the ground, the accuracy of the bore, the temperature of the piece, and the tight or loose fit of the bullet. This multitude of circumstances was demarcated outside the realm of the mathematician’s endeavour; although some might be subject to rules, their handling was best referred to practice and the discretion of the gunner.
From the complex reality of gunnery Digges therefore abstracted just four factors for discussion: powder, piece, bullet and randon. In his 1579 series of questions on artillery his aim was to both isolate and interrelate the effects of each. Powder came in several forms, for example, serpentine and corned. Each type had [page 98:] different characteristics, while the quantity of powder also affected the range of shot. Concerning the piece, both the length and the proportion of its hollow cylinder were apparently related to performance. The bullet itself might be made of stone, iron, or lead; the different densities of these materials meant that both size and weight came into play in determining the resultant motion. Finally there was the piece’s angle of elevation, the randon, and its very visible affect on both the form and range of the projectile’s motion.
These general effects were clear, but Digges did not want to leave the art at the level of qualitative interrelation. The questions which he proposed in 1579 were intended to raise the possibility of a geometrically precise ‘theoric’ and it was the topic of randons which offered the greatest scope for mathematical solution. For Digges, the determination of randons and ranges was the pinnacle of the art, ‘wherein only consisteth the chief difficulties and rarest mysteries of this new science or art of great artillery’ (1590: 368).
Leonard had already tackled some of the problems. He had rejected Tartaglia’s claim that 45° was the angle of utmost randon (the angle giving greatest range), for in practice the utmost randon was found to be several degrees less.67 Moreover, the argument for the importance of 45° had been based simply on its half-way position between the horizontal and the vertical. Leonard considered that the utmost randon was not half of 90° but half of the angle at which an artillery piece [page 99:] gave the same range as the horizontal ‘point blank’ distance (1590: 366). Thomas followed his father on this question of utmost randon, but does not appear to have inherited so definite a doctrine concerning the form of the ballistic curve.
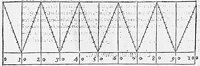
Like many others who concerned themselves with gunnery, Leonard and Thomas began with Tartaglia’s account of the bullet’s path. Tartaglia had distinguished three elements of the projectile’s trajectory: an initial straight line, a curving section, and a final right line down to the horizon.68 However, Leonard denied Tartaglia’s claim that the curving section was an arc of a circle. His own solution may be that preserved in his son’s artillery questions of 1579. Thomas asked whether the curved part of the trajectory was not rather a conic section: a parabolic arc for the utmost randon, an elliptical arc for lower elevations, and a hyperbolic arc for higher (1579: 187-8). This neat solution reflected the geometric generation of conic sections by the intersection of a variably inclined plane and a cone.
Flexible and ingenious as this theory was, it nevertheless did not retain Thomas’s favour. In the second edition of Stratioticos the artillery questions were not only reprinted but in many cases resolved by the addition of marginal answers. Whereas most of the answers were a simple yes or no, the series of questions on the curved part of the bullet’s path merited a different response. After first rejecting Tartaglia’s circular arc, Digges had originally asked whether the upper part of the bullet’s circuit was a conic section. He now responded: ‘Nearer but not perfect conical, but rather helical’ (1590: 356). No reply was made to the succeeding specific [page 100:] questions on ellipses, parabolas, and hyperbolas. Digges simply reiterated his conclusion alongside the final question: ‘Albeit all these randon arcs be helical and not perfect conical, yet they have a very near resemblance’ (1590: 357).
Not surprisingly, the margin of Stratioticos could accommodate no more than these brief statements. Digges outlined his ‘helical’ replacement for the artillery application of conics in an appendix to the second edition of Pantometria (1591). This addition consisted of a preface, 20 definitions (said to be from the third book of the promised artillery treatise), another 20 definitions (from book five), and 51 theorems, ‘resolving the most part of my artillery questions in Stratioticos proponed’ (1591: 181). Digges explained that the bullet’s trajectory is compounded of two motions, the first a violent one directed in a straight line out of the piece and the other a natural one striving downwards perpendicular to the horizon. The composition of the two motions creates the mixed helical circuit (1591: 180). Digges made it clear that his inspiration was derived from Archimedes’s On spirals. In that text the ancient geometer generated his spirals as the locus of a point moving uniformly on a radius which is itself uniformly turned about its circle’s centre.69 Digges’s helical circuits were therefore analogous rather than identical for they were composed of two right line motions rather than a right and circular.70 [page 101:]
However there was another, much more familiar, context in which motions were compounded: astronomy. The machinery of epicycles had been specifically designed to produce a composite motion from two circular motions. Digges dallied with this alternative treatment of compounded motions, drawing an explicit parallel with artillery problems. He referred to astronomers’ epicycles and eccentric circles as a counterpoint to the helical arcs required for artillery (1590: 367-8). But beyond introducing astronomical language and techniques to emphasise the complexity of artillery problems, he stated that the methods themselves could be directly imported, ‘to discover and find out these helical motions’ (1591: 180).
Digges’s brief artillery references to astronomy point up both the continuities and the contrasts between his early and later mathematical work. In the early 1570s Digges had valued astronomy as a high and difficult art. Yet at the end of his career he introduced it not for its own sake, but only to elucidate the science of great artillery. Astronomy, rather than being placed at the peak of mathematical endeavour, had become a subsidiary affair, supplanted by the more significant military art. Moreover, the high status now accorded artillery was due to its utility in the defence of prince and country, rather than to the elevated character of its objects.
Digges now sympathised with his father’s determination to produce profitable matters, ‘rather than by difficult and curious demonstrations to stir up an admiration of his knowledge’ (1591: 80). Thomas’s pursuit of artillery was likewise immune from any imputation of mere intellectual vanity; the same had perhaps not been said of his work on geometrical solids and parallactic astronomy. But artillery did not satisfy only Digges’s sense of gentlemanly responsibility. It was especially valued because in it he could combine useful knowledge with the rare and novel matter which [page 102:] he had sought out from his earliest publications: the study of artillery demonstrated that Apollonian conics and Archimedean spirals were not mere toys but could assist in the most weighty of affairs. Military necessity and commodity both sustained and redirected Digges’s aspiration to higher things.
But if Digges’s desire for rarity and difficulty in mathematics allows us to see some element of continuity with his earlier mathematical role, the decidedly military character of artillery marks a larger distinction. Artillery was pursued within a broader programme of military engagement which included active service and the prescription and revision of military ordinances. Its first association was with the ideology of the active gentleman. Whatever the attractions of demonstrative discourse, Digges tackled artillery in order to achieve results.
In studying artillery Digges was redefining his identity and creating a role for himself as a mathematical practitioner. This shift carried through even into his choice of language. Mathematical practice was a vernacular phenomenon. Yet though Digges had published his Mathematical Discourse (1571) in English to accompany Leonard’s Pantometria, his next publication had been the Latin Alae (1573). Digges knew that if he published his artillery treatise in Latin he would
greatly amplify mine own fame and the admiration of such rare mathematicians as at this day live in several nations of Christendom, from whom I have for far inferior inventions imprinted in my treatise entitled Alae seu scalae mathematicae already received no small applause; yet, if I publish the same at all, I do constantly resolve to do it only in my native language (1591: 176).
Digges’s 1591 decision to avoid Latin for his work on artillery was meant to prevent his militarily sensitive conclusions from spreading too widely among other [page 103:] nations. Yet he was not narrowly nationalistic here. Digges also intended his work to enrich the vernacular, increasing its importance so that it would be more highly regarded by foreigners. As a learned practitioner, Digges sought to serve prince, country and religion not only by mathematically ridding contemporary practice of errors and establishing new results, but even by promoting the language of the commonwealth.
5. THE MAKING OF A MATHEMATICAL PRACTITIONER
Thomas Digges’s own references to his move from ‘demonstrative contemplations to experimental actions’ have been at the centre of my interpretation of the changing pattern of his career. But rather than relying on Digges’s own language of contemplation and action, I have shifted the explanatory burden onto the two gentlemanly ideals to which mathematics was successively attached. Inevitably, in such a limited space, my interpretation has focused all but exclusively on Digges himself. But of course he did not reformulate his own role in splendid isolation: his commitments were socially renewed.
Digges’s moral and political conscience was reconstructed in the intensely communal environment of parliament and among the self-consciously virtuous clientage of the Earl of Leicester. He gravitated towards a milieu in which his beliefs were approved and he was personally given honour and credit. With praise and favourable acceptance from both noblemen and upright gentlemen, Digges extended his activities in the directions valued by his like-minded peers. In stressing how crucial was Digges’s unavoidable social identity as a gentleman, and how his [page 104:] participation in ruling society is essential to the form of his career and role, we are nevertheless still not so far from Digges’s own self-understanding. In the preface to Stratioticos, he recalled how he had ‘spent my youngest years, even from my cradle, in the sciences liberal, and especially in searching the most difficult and curious demonstrations mathematical.’
Yet finding none, or very few, with whom to confer and communicate those my delights, (and remembering also that grave sentence of divine Plato, that we are born not for ourselves, but also for our parents, country, and friends), after I grew to years of riper judgement, I have wholly bent myself to reduce those imaginative contemplations to sensible practical conclusions, as well thereby to have some companions of those my delectable studies, as also to be able, when time is, to employ them to the service of my prince and country (1579: A3r-v).
Digges projects the social formation and inculcation of his newly defined role as a mathematical practitioner onto the plane of personal choice. In contrast, my account of his development as an active, virtuous gentleman has restored a formative dimension to his immediate society. Inevitably, a fuller account would need to move beyond Digges himself to some of his ‘companions’, those men struggling to articulate and realise similar ideals. But rather than attempting any such larger account here, I will conclude with just a single example, as a way of pointing to the network of associations which motivated and sustained Digges.
One of Digges’s colleagues in parliament was Sir Philip Sidney. As a fellow client of the Earl of Leicester, Sidney shared Digges’s strong Protestantism and his interventionist foreign policy. Not only did they serve together on parliamentary committees, but Digges travelled to the Netherlands with Sidney in 1585.71 [page 105:] Moreover, in the field of poetry and prose, Sidney was attempting to define a parallel transition to that of Digges in the mathematical arts: the initial version of Arcadia, his chivalric romance, was later reworked to serve more didactic and epic ends.72
In his Apology for Poetry, Sidney aptly (if inadvertently) indicates that Digges was not alone in his efforts to redefine a new and self-consciously virtuous identity. Sidney managed to capture the values prompting Digges’s early work in his claim that all the arts and sciences have a single aim:
to know, and by knowledge to lift up the mind from the dungeon of the body to the enjoying of his own divine essence ...[to] lead and draw us to as high a perfection as our degenerate souls, made worse by their clayey lodgings, can be capable of.73
However, different people, pursuing different arts, have gone about this task differently:
For some that thought this felicity principally to be gotten by knowledge, and no knowledge to be so high and heavenly as acquaintance with the stars, gave themselves to Astronomy; others, persuading themselves to be demi-gods if they knew the causes of things, became natural and supernatural philosophers; some an admirable delight drew to Music; and some the certainty of demonstration to the Mathematics.
Sidney’s list palpably resonates with Digges’s early work. Even the title page of Alae proclaims how Digges’s mathematical wings will raise the reader upwards to the heavens, while the demonstrative character of mathematics is repeatedly underlined in both Alae and the Mathematical Discourse. [page 106:]
But Sidney also articulated the values of Digges’s later career, for he had come to realise that knowledge alone was ultimately insufficient. Rather, the ‘ending end of all earthly learning [is] virtuous action’. The highest object of learning lies ‘in the knowledge of a man’s self, in the ethic and politic consideration, with the end of well-doing and not of well-knowing only.’ Well-doing and not well-knowing only: this represents the point on which Thomas Digges’s gentlemanly shift of mathematical allegiance turned.
FOOTNOTES
1. For a (generally reliable) brief biographical account, see C.C. Gillispie (ed.), Dictionary of Scientific Biography, 16 vols (New York, 1970-80), IV, pp. 97-8. For Digges’s astronomy: Francis R. Johnson and Sanford V. Larkey, ‘Thomas Digges, the Copernican system, and the idea of the infinity of the universe in 1576’, Huntington Library Bulletin, 5 (1934), 69-117 (which reprints the Perfit Description), Francis R. Johnson, Astronomical Thought in Renaissance England: a Study of the English Scientific Writings from 1500 to 1645 (Baltimore, 1937), esp. chh. 5 and 6, Alexandre Koyré, From the Closed World to the Infinite Universe (Baltimore, 1957), pp. 34-9. For a more recent example of Digges’s place within the story of astronomy, René Taton and Curtis Wilson (eds), Planetary Astronomy from the Renaissance to the Rise of Astrophysics: Tycho Brahe to Newton (General History of Astronomy, vol. 2A) (Cambridge, 1989), pp. 22-3. For an example of Digges’s place in an account of the Scientific Revolution, A.R. Hall, The Scientific Revolution (London, 1954), p. 104.
2. D.W. Waters, The Art of Navigation in Elizabethan and Early Stuart Times (London, 1958); A.W. Richeson, English Land Measuring to 1800: instruments and practices (Cambridge, Mass., 1966); A.R. Hall, Ballistics in the Seventeenth Century (Cambridge, 1952); H.J. Webb, Elizabethan Military Science: the Books and the Practice (Madison, 1965).
3. On Leonard, Dictionary of Scientific Biography (footnote 1), IV, p. 97.
4. In-text references to Digges’ publications are keyed by the year of publication and the page number or signature.
5. Digges did publish two short and ephemeral military narratives late in his career: H.J. Webb, ‘Two additions to the military bibliography of Thomas Digges’, Modern Language Quarterly, 12 (1951), 131-3.
6. Even otherwise careful historians have merged Leonard and Thomas into a single, undifferentiated identity, the Digges; for an example, Charles B. Schmitt, John Case and Aristotelianism in Renaissance England (Kingston, 1983), p. 47. John Dee further complicates the father-son relationship for, after Leonard’s death, he acted as some form of tutor to Thomas. Thomas refers to Dee as his ‘second mathematical father’ in the preface to Alae (1573: A2r) and also in his preface to Dee’s Parallaticae Commentationis Praxeosque Nucleus Quidam (London, 1573), A2r. In the latter work, Dee himself calls Digges his ‘most worthy mathematical heir’ (A2v). However, the precise details of their relationship are not known.
7. E.G.R. Taylor, Mathematical Practitioners of Tudor and Stuart England (Cambridge, 1954), p. 175 for Digges’s biographical entry. Digges’s high-handedness is strongly implied by Taylor’s introduction to A Regiment for the Sea and other Writings on Navigation by William Bourne, Hakluyt Society, 2nd series, 121 (Cambridge, 1963), p. xxxii, and cf. p. xiii.
8. There is a large and rapidly growing literature on Renaissance patronage. For a useful entry to the literature, particularly oriented towards the history of science, see Bruce T. Moran (ed.), Patronage and Institutions: Science, Technology, and Medicine at the European Court, 1500-1700 (Woodbridge, Suffolk, 1991).
9. Mordechai Feingold, The Mathematicians’ Apprenticeship. Science, Universities and Society in England, 1560-1640 (Cambridge, 1984), p. 186, and cf. 206-7. Similarly, F.R. Johnson had earlier explained the shift of direction announced by Digges in 1579 as the outcome of compulsion (footnote 1), p. 179. (Note too that Feingold’s implicit opposition between theoretical and practical phases of Digges’s career remains tied to the terms of Digges’s own contrast between contemplation and action. My study suggests that such an approach effectively precludes a full understanding of Digges’s career.)
10. Robert Hovenden (ed.), The Visitation of Kent taken in the years 1619-21, Harleian Society, 42 (London, 1898), pp. 64-5 prints a genealogy of the Diggeses. For Kent society, Peter Clark, English Provincial Society from the Reformation to the Revolution: Religion, Politics and Society in Kent 1500-1640 (Hassocks, Sussex, 1977).
11. For the Wyatt rebellion and Leonard’s part in it, David Loades, Two Tudor Uprisings (Cambridge, 1965) and G.R. Elton, England Under the Tudors, second edition (London, 1974), p. 217. For the details of Leonard’s case, Calendar of Patent Rolls, Philip & Mary, I (1553-4), pp. 261, 266 and II (1554-5), pp. 270-1.
12. The Statutes of the Realm, IV (1819; repr. London, 1963), p. xxvi and Commons Journals, I, pp. 66, 67, 69.
13. See especially Steven Shapin, ‘"A scholar and a gentleman": the problematic identity of the scientific practitioner in early modern England’, History of Science 29 (1991), 279-327.
14. Despite its title, C.D. Hellman, The Comet of 1577: its Place in the History of Astronomy (New York, 1944) also provides a review of responses to the 1572 new star.
15. PRO SP12/90/12, dated 11 December 1572. Note that the letter was only written because Digges was too unwell to attend Burghley in person, and also that Digges was still uncertain whether the phenomenon was a comet or a genuine star.
16. BL Lansd. MS 19/30, printed in James Orchard Halliwell (ed.), A Collection of Letters Illustrative of the Progress of Science in England (London, 1841), pp. 6-7. Halliwell does not print the endorsement by Burghley’s secretary ‘14 May 1574. Mr Digges to my Lord presenting his book’.
17. The precise form of this ‘frame’ is not known. It is mentioned by Jacob Rathgeb, who recorded the 1592 visit to England by Frederick, Duke of Wurttemburg: Kurtze und Warhaffte Beschreibung der Badenfahrt (Tubingen, 1602), ff. 32v-33r, translated in W.B. Rye, England as seen by Foreigners in the Days of Elizabeth and James the First (London, 1865), p. 44. For Theobalds, John Summerson, ‘The building of Theobalds, 1564-1585’, Archaeologia, 97 (1959), 107-26.
18. On Digges’ poetic accomplishments, note that he had learnt one book of Palingenius’ Zodiacus Vitae by heart and took ‘much delight to repeat it often’ (G.C. Moore Smith, Gabriel Harvey’s Marginalia (1913) p. 161). Digges also made a habit of quoting Palingenius in print: preface to Perfit Description (1576), preface to Stratioticos (1579) as well as second edition (1590), p. 364. Note too that John Dee had composed a similar work on ‘The Philosophical and Poetical Original occasions of the Configurations and names of the heavenly Asterismes’, presented to the Duchess of Northumberland in 1553: Nicholas H. Clulee, John Dee’s Natural Philosophy: Between Science and Religion (London, 1988), p. 31.
19. On the design and decoration of gardens, Roy Strong, The Renaissance Garden in England (London, 1979), which notes the importance of sundials as garden furniture.
20. For Digges’s election, P.W. Hasler (ed.), The House of Commons 1558-1603, 3 vols (London, 1981), II, p. 37. On the character and context of entry to parliament, Mark Kishlansky, Parliamentary Selection. Social and Political Choice in Early Modern England (Cambridge, 1986). For the dramatic rise in the proportion of gentry taking seats in 16th century parliaments, J.E. Neale, Elizabeth I and her Parliaments, 2 vols (London, 1953-1957), I, p. 21. A more measured characterisation of the significance of this change is given by G.R. Elton, ‘Tudor Government: the Points of Contact I. Parliament’, Transactions of the Royal Historical Society, 5th series, 24 (1974), 183-200.
21. On the character of the early Elizabethan parliaments, G.R. Elton, The Parliament of England 1559-1581 (Cambridge, 1986). For Digges’s paper against Norfolk, who was accused of traitorous involvement in the Ridolfi Plot against Elizabeth, T.E. Hartley (ed.), Proceedings in the Parliaments of Elizabeth I, 1558-1581 (Leicester, 1981), pp. 294-5.
22. Commandino reviewed this debate in the introduction to his Latin translation of Euclid (Urbino, 1572).
23. Digges certainly treated these last two books as integral with the rest of the text. He refers to the 15 books of Euclid’s Elements and talks of the five last books of solids (see 1571: Aa1r, for example).
24. For a summary of their content, Thomas L. Heath (ed.), The Thirteen Books of Euclid’s Elements, 3 vols (New York, 1956), III, pp. 512-520.
25. For Piero’s account, see G. Mancini, ‘L’opera "De corporibus regularibus" di Pietro Franceschi detto Della Francesca, usurpata da Fra Luca Pacioli’ Atti della R. Accademia dei Lincei. Memorie della Classe di Scienze Morali, Storiche e Filologiche, series 5, volume 14, fasc. 7B (1916); the additional inscription is the icosahedron in a cube, see p. 543 (proposition III, 4).
26. Pappus recorded Archimedes’s discovery of the solids in book V of his Collection. On the transmission of the Archimedean solids, see Marshall Clagett, Archimedes in the Middle Ages, 5 vols (Madison/Philadelphia, 1964-84), III, iii, pp. 398-406, 455-8.
27. For example, Piero della Francesca, as printed in Luca Pacioli, Divina Proportione (1509), Albrecht Dürer, Underweysung der Messung (1525) and Daniele Barbaro, La Pratica della Perspettiva (1568). The last two are graphical treatments, showing nets which can be cut out and folded to give the solids.
28. Jofrancus Offusius, De divina astrorum facultate in larvatam astrologiam (Paris, 1570), ff. 3r-5r. For Offusius and his English connection with John Dee, see Owen Gingerich and Jerzy Dobrzycki, ‘The master of the 1550 radices: Jofrancus Offusius’, Journal of the History of Astronomy, 24 (1993), 235-254.
29. Koyré (footnote 1) was particularly guilty of this.
30. In stressing Digges’s conviction of the radical divide between the terrestrial and celestial, I differ from Johnson and Larkey’s interpretation. Wishing to present Digges as an exemplary anti-Aristotelian, they attempted to explain away his use of the distinction, seeing it as no more than a sop to his readers (footnote 1), pp. 101-2. This is to misconceive an essential element of Digges’s intellectual order.
31. I have run together the characterisation in this paragraph from various passages in Alae seu scalae mathematicae and the Perfect Description. Alae: A1v (the beautiful order of the heavenly bodies), A2r (the unchanging pure aether), A3v (no substantial change in the heavens), and L2v (our troubled life on this dark and obscure terrestrial star). Perfect Description: the diagram and its captions (the earth as the globe of mortality compared to the perfect joy of the habitacle for the elect), M2r (quotations from Palingenius’s Zodiacus Vitae), N4r (‘our Elementare corruptible world’ matched against ‘the glorious court of the great god’). Note that, in the preface to Pantometria, Digges had earlier contrasted Atlas’s imprisonment in a mortal carcass here in this most inferior and vile part of the universal world with the pleasant and beautiful frame of celestial orbs (1571: A3r).
32. E.M.W. Tillyard, The Elizabethan World Picture (Harmondsworth, 1963), p. 26, Carol Z. Wiener, ‘The Beleaguered Isle. A study of Elizabethan and early Jacobean anti-Catholicism’, Past and Present, 51 (1971), 27-62, p. 41, and Joel Hurstfield, The Elizabethan Nation (London, 1964), esp. pp. 37, 91.
33. Cf. 1579: a1r. For more on the relations between mathematical astronomy and natural philosophy in the learned circles of the 16th century, see N. Jardine, The Birth of History and Philosophy of Science (Cambridge, 1984), esp. ch. 7.
34. Latin text and translation of Regiomontanus in Jane L. Jervis, Cometary Theory in Fifteenth-Century Europe (Dordrecht, 1985).
35. Alae, 2A3v-2A4r, B2r-v, L1v-L2r. Tycho would later criticise Regiomontanus’ method in identical terms; see Victor E. Thoren, The Lord of Uraniborg. A Biography of Tycho Brahe (Cambridge, 1990), p. 263.
36. A reconstruction by John J. Roche; see his paper ‘The radius astronomicus in England’, Annals of Science, 38 (1981), 1-32, p. 21. Roche’s study gives more information on both Digges’s and other mathematicians’ versions of the radius.
37. Digges attributed the transversal method of division to the navigator and mechanician Richard Chancellor, who had been an associate of Dee (1573: K3r). Tycho had an independent source for his use of transversals and their use had been described long before by Levi ben Gerson, on whom see B.R. Goldstein, The Astronomy of Levi ben Gerson (New York & Berlin, 1985), pp. 55, 146-9.
38. David H. Clark and F. Richard Stephenson, The Historical Supernovae (Oxford, 1977), ch. 10, pp. 185-6.
39. Bibliothèque Publique et Universitaire, Geneva, shelfmark Kb 467. My thanks to Owen Gingerich for supplying information on this copy.
40. 1576: M1r. Whether Digges’ reference to astronomy as philosophy was deliberate or just loose usage is uncertain. But he did repeat the phrase by writing of ‘this most excellent and difficult part of philosophy’ (1576: N1r).
41. For Digges’s elections, Hasler (footnote 20), II, p. 37. Parliamentary dates: ibid., I, pp. 77, 81.
42. Joan Simon, Education and Society in Tudor England (Cambridge, 1966/1979), p. 357.
43. Digges features in a series of papers by Michael Graves identifying and discussing the phenomenon of the ‘man of business’. See especially ‘The Management of the Elizabethan House of Commons: the Council’s Men-of-Business’, Parliamentary History, 2 (1983), 11-38; ‘Managing Elizabethan Parliaments’, in D.M. Dean and N.L. Jones (eds), The Parliaments of Elizabethan England (Oxford, 1990), 37-63; and note also his The Tudor Parliaments: Crown, Lords and Commoners, 1485-1603 (London, 1985), 148-9. Patrick Collinson has emphasised that Digges and his colleagues were not mere passive tools of the Privy Council but were actively following their own political and religious agendas: ‘Puritans, Men of Business and Elizabethan Parliaments’, Parliamentary History, 7 (1988), 187-211. For an example of a motion adopted and advocated by Digges, R. Hitchcock, A Pollitique Plat (London, 1580), especially last page and Sir Simonds D’Ewes, The Journals of all the Parliaments during the reign of Queen Elizabeth (London, 1682; facsimile, Shannon, 1973), p. 290. For the context of Hitchcock’s plat, G.R. Elton, ‘Piscatorial politics in the early parliaments of Elizabeth I’, in N. MacKendrick and R.B. Outhwaite (eds), Business Life and Public Policy. Essays in Honour of D.C. Coleman (Cambridge, 1986), 1-20.
44. BL Lansd. 43/72, f. 169v.
45. For his committee work, Hasler (footnote 20), II, pp. 37-8.
46. For Digges and Dover, see chapter 5.
47. BL Lansd. 119/9; PRO SP12/176/26 (copies at SP12/176/27 and BL Lansd. 98/4); and SP12/176/32. On Digges’s discussion of an Interregnum to secure the succession to Queen Elizabeth, Patrick Collinson, ‘The Monarchical Republic of Queen Elizabeth I’, Bulletin of the John Rylands University Library, 69 (1986-7), 394-424. Two ‘military paradoxes’ by Digges, first published posthumously in 1604, may have been written at this time. One exists in manuscript: BL Lansd. 98/6.
48. Cf. Wiener (footnote 32) and Peter Lake, ‘The significance of the Elizabethan identification of the Pope as antichrist’, Journal of Ecclesiastical History, 31 (1980), 161-78.
49. Simon Adams, ‘Faction, clientage, and party: English politics 1550-1603’, History Today, 32 (December 1982), 33-39.
50. W.T. MacCaffrey, Queen Elizabeth and the Making of Policy, 1572-1588 (Princeton, 1981) and Simon Adams, ‘A Puritan crusade? The composition of the Earl of Leicester’s expedition to the Netherlands, 1585-1586’, in P. Hoftijzer (ed.), The Dutch in Crisis, 1585-1588: People and Politics in Leicester’s Time (Leiden, 1988), 7-34, p. 10.
51. SP83/9/7, printed in J. Kervyn de Lettenhove, Relations Politiques des Pays Bas et de l’Angleterre, 11 volumes (Brussels, 1882-1900), 10 (1891), 794-796. The letter is dated from Antwerp, 4 September 1578. The exact purpose of Digges’s visit is unclear though, from the references to the Prince of Orange, Digges may have been acting as a diplomatic go-between.
52. Note that Leicester acted as Digges’s patron for nomination to the 1584 parliament: A.L. Merson (ed.), The Third Book of Remembrance of Southampton 1514-1602, 4 volumes (Southampton Records Series, 1952-79), III, p. 34. For Leicester as a parliamentary patron, Simon Adams, ‘The Dudley clientele and the House of Commons, 1559-1586’, Parliamentary History, 8 (1989), 216-39 and for a wider discussion of Leicester’s patronage, see Eleanor Rosenberg, Leicester, Patron of Letters (New York, 1955).
53. BL Harleian MS 6993/49. Digges reiterated his desire to serve when responding to a September 1585 request from Francis Walsingham for information on the town of Sluis; SP84/3/99.
54. SP84/27, f. 63r. This document is a later autobiographical account of Digges’s Low Countries service.
55. J. Bruce (ed.), Correspondence of Robert Dudley, Earl of Leycester, During his Government of the Low Countries, in the years 1585 and 1586, Camden Society, 27 (London, 1844), p. 135; Leicester to Walsingham, February 1586. For a modern appraisal of Digges as muster master, see C. Cruickshank, Elizabeth’s Army, second ed. (Oxford, 1966), p. 136.
56. Calendar of State Papers, Foreign, 21 (2): 1586-7, p. 172.
57. Calendar of State Papers, Foreign, 21 (4): 1588, p. 87.
58. SP15/31/142: Digges to Burghley, 2 May 1590. Cf. James Digges to Burghley, March 1590; List and Analysis of State Papers, Foreign, 1: 1589-90, p. 185.
59. A Briefe Report of the Militarie Services done in the Low Countries, by the Erle of Leicester (London, 1587).
60. A Briefe and true report of the Proceedings of the Earle of Leycester for the reliefe of the towne of Sluce (London, 1590). This text was printed for inclusion in the second edition of Stratioticos but was also issued separately.
61. SP15/31/151: 24 July 1590, enclosing a ‘conference’ of a good and bad muster master such as was to appear in the revised second edition of Stratioticos.
62. The novelty of Digges’s emphasis on the learning appropriate to a general is noted by Webb (footnote 2), p. 55.
63. Stratioticos was preceded by the lost first edition of William Bourne’s Art of Shooting (1578), and followed by a range of other texts, including the unpublished work of Thomas Bedwell (for which, see chapter 4).
64. A brief account of Leonard’s work on great ordnance survives in Pantometria (1571: I4r-v). Leonard had practical and theoretical skills in artillery as early as 1542, see SP1/171, f. 29r (Letters and Papers Foreign and Domestic of the Reign of Henry VIII, 17, p. 234, article 405).
65. 1590: 362. For Digges’s diagnosis of errors, see 1579: 65-6, 189 and 1590: 362-8.
66. For general accounts, which also discuss the Diggeses, see Hall (footnote 2) and Henry J. Webb, ‘The science of gunnery in Elizabethan England’, Isis, 45 (1954), 10-21.
67. The modern theory of projectiles, inaugurated by Galileo, would accept that 45° was the correct angle of utmost randon, assuming no air resistance or other effects. In Two New Sciences, Galileo gave only theoretical ranges and neglected the disturbing accidents and effects encountered in practice; for him, the departure from 45° was due only to the ‘impediments of matter’ and could not be encompassed by mathematical theory. While Thomas and Leonard also abstracted from messy reality, they had a commitment to a closer representation of ballistic phenomena.
68. For Tartaglia’s account, see S. Drake and I.E. Drabkin (eds), Mechanics in Sixteenth-Century Italy (Madison, 1960). Thomas would later reject the idea that there was a distinct straight section of the projectile’s trajectory, though for practical purposes of calculation he allowed it to be retained (1591: 167 [sic], theorems 13 and 15).
69. E.J. Dijksterhuis, Archimedes (Princeton, 1987), ch. 8. Digges was already familiar with the combination of circular and straight motions in the 1570s; note his discussion of the motion of a plummet falling on board a ship (1576: O2r). Also compare his discussion of the mariner’s plain chart, on which every direction other than the four cardinal points should be represented not by a straight line but by ‘a curve or helical line, neither straight nor circular, but mixed of both’ (1576: P1r).
70. 1591: 168 [sic], theorem 21, with reference to Archimedes. Note that Digges had already made a seemingly offhand reference to helical motions in 1579. Just after citing Archimedes as an expert mathematician he mentioned the ‘mixed helical arc or circuit of the bullet, componed of violent and natural motions’ (1579: 188). But Digges made no attempt to juxtapose this suggestive remark with his questions on conic sections and the ballistic trajectory.
71. On Sidney in parliament, Hasler (footnote 20), III, pp. 382-4. For the crossing to the Netherlands, SP84/27, f. 63r.
72. For the transformation of Arcadia, see the introduction to Sir Philip Sidney, The Countess of Pembroke’s Arcadia, edited by Maurice Evans (London, 1977), esp. pp. 12, 20.
73. Philip Sidney, An Apology for Poetry, ed. G. Shepherd (London, 1965), p. 104 (the following quotations from Sidney also come from this page). Cf. the remarkably similar comments in the Preface to Pantometria (1571), A3r-v.