Rome revisited: the vertical disc dial
Introduction
The image shows a Roman portable sundial in the collection of the Museum of the History of Science, Oxford (inv. 51358). It is one of several Roman and Byzantine examples of this type of vertical dial to survive.
I was directed to these dials by a research visit to the collection at Oxford by two classicists. My academic visitors may not have realised the depth of my own surprise when I couldn’t provide a satisfactory explanation of the dial’s operation. It is normally possible to grasp the workings of a dial on the hoof, because it conforms to the familiar geometry of the sun’s apparent motion. Moreover, this dial is compact and neatly executed: surely it should be straightforward in operation? But while it would clearly indicate midday when correctly arranged for both latitude and date, beyond this it was confusing. While I could see roughly how it worked in the morning, its afternoon configuration appeared to be downright wrong, clashing with the geometry of the celestial sphere.
There is a literature on these dials. Frederick Stebbins, ‘A Roman Sun-Dial’, Journal of the Royal Astronomical Society of Canada, 52 (1958), 250-4 specifically focuses on the Oxford example as an example of the general type. A more recent and comprehensive treatment has been given by Michael Wright: ‘Greek and Roman Portable Sundials: An Ancient Essay in Approximation’, Archive for History of Exact Sciences, 55 (2000) 177–187 (available online to SpringerLink subscribers). Wright summarises the historical evidence and gives a clear and detailed mathematical exposition of the dial’s form, particularly highlighting its remarkable and distinctive character. Whereas all standard dials are (at least in principle) exact, this form is necessarily approximate.
Yet even after reading these papers I was left with a lingering doubt: I still could not visualise how the dial worked in the afternoon. Sundials are normally symmetrical about midday, since the sun rises in the morning and (near enough as makes no difference) descends in a mirror image in the afternoon. But this dial’s afternoon configuration is rotated, not reflected, so that it no longer clearly matches the heavens. Both Wright and Stebbins focus their attention on the morning, referring only in passing to the afternoon operation. Wright says that because the dial ‘may be regarded as an altitude dial, it works just as well’ in the afternoon as the morning (p. 178) - but does not expand on this further. Stebbins’ account is similar but more discouraging: ‘As the dial simply measures the sun’s altitude, it follows that it can also handle the problem in the afternoon without change of setting, but analysis is more complicated’ (p. 253).
For those who can immediately grasp the way in which the dial's indication of time depends on solar altitude, there is no need to read further. Lacking such insight I decided to construct a larger-than-life version of the dial (fixed for the latitude of Oxford) so as to gain some experience of its operation. Reinforced by the hands-on confidence of seeing the dial actually work, I then returned to the mathematics of the dial, to attempt an analysis of its performance in general terms - for the afternoon as well the morning.
The successful completion of that analysis - agreeing with Wright’s derivation by a different route - was the most that I had expected from this exercise. But then, after this extensive afternoon detour, a genuinely historical conclusion emerged. Wright emphasises the approximate character of the dial, but shows that this would have scarcely registered within the time consciousness of the period. However, any original user with some elementary instruction in the doctrine of the sphere would have appreciated a different sort of problem - not one of practical accuracy but of principle. Realising that the dial approximates the geometry of the sun’s apparent motion in the morning, but does not in the afternoon, some fraction of its users would have registered this as a conceptual puzzle. No doubt for most, indeed the vast majority, the fact that it worked at all was quite sufficient. But at least some of its users must have reflected on its ambiguous status: a tiny pocket device which both depends on the conventional understanding of the sphere and yet inadvertently challenges its universal role.
In the following account I try to pinpoint this conceptual issue and to rework the geometry of the dial and its hour system. If my use of modern trigonometry is anachronistic I nevertheless hope that this account will illuminate the instrument and make it more accessible to others, whether classicists, historians of mathematics and science, or diallists.
Brief description
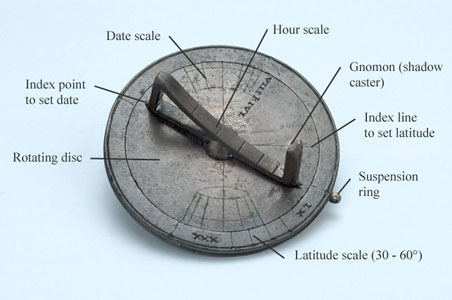
The working parts of the dial are indicated above. In use, the inner rotating disc is turned until its index line is correctly set on the outer latitude scale (users need to know their latitude). Then the dial is set for the date by turning the vane until the pointers indicate the right position on the two symmetrical date scales. The diameter which joins the two scales (which look like a pair of truncated cones) represents the spring and autumn equinoxes when the sun has 0° declination. This diameter bisects the two date scales, which run from the winter solstice at one side of the ‘cone’ (marked ‘VIII K IAN’, eight days before the Kalends of January, i.e. 25th December in the Julian calendar) to the summer solstice at the other side (marked ‘VIII K IVL’, eight days before the Kalends of July, i.e. 24th June). (Wikipedia provides handy background information on the Roman calendar.) The lines between the equinoxes and solstices represent the beginnings of the months.
With the instrument correctly configured for latitude and date, it is then suspended and turned until the shadow cast by the gnomon falls on the hour scale. The user then reads off the time in unequal hours. In the unequal hour system (very common in Europe before the widespread adoption of mechanical clocks), both the daylight period and the night are each divided into 12 equal hours. Except at the equinoxes or all year round on the equator, the day hours are therefore a different length from the night hours. The day begins at sunrise, midday is always 6 o’clock and sunset is 12 o’clock. The dial’s hour scale is for just 6 hours: sunrise to midday or midday to sunset. The 6 hour lines on the scale make equal angles of 15° with the gnomon (so the shape of the scale does not matter – curved in the original, straight in my reconstruction).
The problem
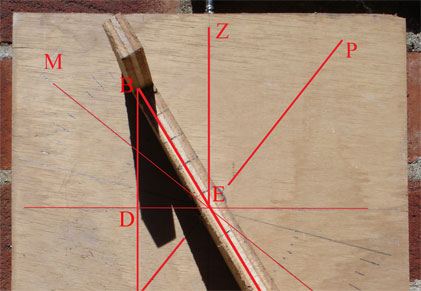
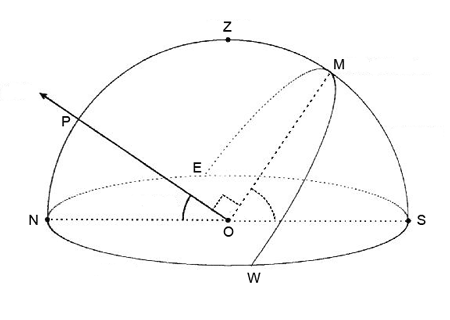To understand why this dial’s afternoon behaviour is not immediately self-evident, we need to see its clearest and most obvious operation – on the morning of the two days in the year when it is exactly right, the spring and autumn equinoxes. On these days the sun moves in the great circle of the celestial equator and rises due east. In the figure the circle NESW is the horizon, with the sun rising at E and moving to M on the meridian at midday. P is the north pole and Z the zenith. The arc EMW is half of the equator, and its plane is at right angles to OP. The latitude θ is the angle between the zenith and the equator ^ZOM, equal to the elevation of the pole above the horizon, ^NOP; ^MOS and ^ZOP are the co-latitude (90 - θ). EM, the sun’s morning arc in the sky, is exactly 90°.
It should be clear from the configuration of the reconstructed dial on this day that its geometry matches the celestial sphere. With the dial facing the eastern horizon, its vane is in the same plane as the arc EM of the sun’s morning passage and, since EM is a quadrant, the unequal hours will be indicated exactly. At sunrise the gnomon points east so that it casts no shadow, while at midday the sun is at M and the shadow of the gnomon is at the top of the vane indicating 6 o’clock.
However, if the dial is turned round after midday until it faces due west, the vane will now be pointing northwards rather than to the south. So in the afternoon it no longer mimics the celestial geometry. How does it work?
The geometry of the dial
First of all we can investigate the apparent time that the dial shows, irrespective of whether it is morning or afternoon, and for any day of the year, not just the equinoxes. The key point here is that, in use, the dial is turned about the vertical axis through Z until the shadow of the gnomon falls on the hour scale. At any instant of the day there is just one orientation which makes the shadow coincide with the scale. With any other orientation the shadow falls elsewhere, as in both the images above, which show the reconstructed dial set for near the summer solstice. In the image on the right the dial has been rotated vertically almost enough to make the shadow coincide with the hour scale. The correct alignment has been achieved in the first picture below. Its neighbour is a close-up with the fundamental geometric diagram of the dial overlaid.
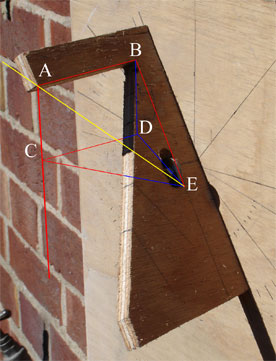
In the marked-up photograph above, yellow is the line to the sun (passing through the tip of the gnomon and projecting beyond the shadow on the hour scale), red represents ‘visible’ construction lines, while those in blue lie behind the plane of the vane. ABCD is a vertical rectangle; triangle CDE is horizontal; and triangle BDE is parallel to the face of the dial.
The time indicated by the dial in unequal hours, h’, can be expressed in terms of the angle ^BAE. Since, as we saw above, the 90° quadrant defined by the gnomon and hour scale is divided into 6 hours,
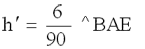
In the diagram, sin ^BAE = BE/AE, while sin ^AEC = AC/AE = BD/AE and cos ^DBE = BD/BE.
Therefore:
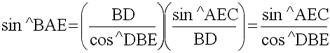
^AEC is the altitude of the sun – the angle between its shadow-casting ray and the horizontal plane. ^DBE is given from the configuration of the dial for latitude and date. Although the dial is differently oriented below (so the shadow no longer falls on the scale), it should be clear that the two triangles DBE match each other (though the one below is displaced slightly to the left). From the photograph below it is clear that ^DBE = ^BEZ = ^MEZ - ^MEB = θ - δ, where θ is the latitude and δ the sun’s declination.
If the solar altitude ^AEC is a, then
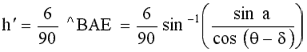
We therefore have the relationship between the time indicated on the dial and the latitude, the date and the height of the sun. This solves my main problem because it shows how, whether in the morning or the afternoon, the dial indicates an hour which depends on the local circumstances of time and place. Even though the dial may follow the celestial geometry only at the equinoxes (and even then only in the morning), the dial has its own fundamental geometrical scheme which holds at all times of the day and year. Moreover, through handling the dial it is clear that, at any one instant, there is only one orientation which brings the shadow into alignment with the hour scale. The dial thus delivers a unique indication of time, just as we would expect, and this behaviour is reflected in the dependence of h’ on the (contantly changing) solar altitude.
It was only after both hands-on experimentation and mathematical derivation that I properly understood Wright’s brief comment that the instrument is an altitude dial. My difficulty arose from the fact that the dial clearly relates to the celestial sphere in the morning, even if it is only exact at the equinoxes (Wright discusses the nature of the approximation for the rest of the year). But it does represent a conceptual departure in the afternoon.
Acknowledgements
Thanks to Matthew Brailsford for help in making the reconstruction (and joining in the ‘sourcing’ of materials in a nearby skip).