An English mathematical aide-memoire of the 17th century
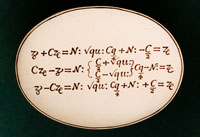

This research note investigates a small silver oval medallion (approximately 48 x 37 mm) held in a private collection. Its provenance is unknown and the details of its context and attribution have not been securely pinned down. Nevertheless the information engraved on its two faces can be interpreted. The object is revealed as a witness to the virtuoso amateur culture of mathematics in 17th-century England.
Face 1: the equations
The image above left shows one face of the object, with three lines of equations. The mathematical notation may no longer be familiar but can easily be deciphered using standard texts of the 16th and 17th centuries. It turns out that the first half of each line represents a particular case of the quadratic equation; the second half (after the colon) represents its solution.
Rewriting the equations in more modern form gives:
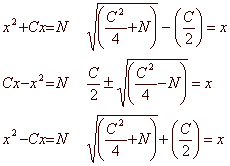
For comparison, students are now taught to solve a general quadratic equation ax2 + bx + c = 0 using a single all-purpose solution:
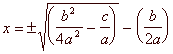
The family resemblance between the early-modern mnemonic and the modern solution should be clear. The medallion presents three particular cases, with the coefficient of x2 always equal to 1, and both the coefficient C and the number N understood to be positive. (The coefficients in the modern standard form can be positive, negative or zero.) The medallion’s three cases are the standard ones for textbooks of the period; in each case only the positive roots (solutions) are given.
The notation used on the medallion is a hybrid. The symbol for the unknown (modern ‘x’) is a form of ‘r’ (for ‘root’, ‘radix’ or ‘res’), while the ‘z’ for square comes from ‘zensus’ or ‘census’, literally meaning ‘wealth’ or ‘excess’. These symbols had been in use from at least the early 16th century, and had first been published in English in Robert Recorde’s Whetstone of Witte (London, 1557). They began to be displaced from the 1590s firstly by François Viète’s notation of Aq, Ac, etc (for squares and cubes) and then latterly (after 1637) by the modern index notation. While the medallion does not use index notation, two of its solutions do use Cq for C2.
The modern root symbol √ appears, qualified by a ‘q’ to show that it is a square root. In the sequence √qu: the ‘u’ stands for universal and indicates that the square root operates over all the terms between the first and second colons. Equations in this form appear in William Oughtred’s Clavis Mathematicae; for example, on p. 89 of the English edition of 1647 we find √u:¼BKq + 2CAq: + ½BK = BC.
Face 2: the tables
This side of the medallion was initially the more obscure of the two. However, the words at the bottom of the two main columns of numbers (‘Dayes’ and ‘Months’) provided the most obvious evidence that this is an English object.
The mathematical structure of the tables was cracked by Rob van Gent, and it then became clear that this numerical table was intended to simplify calculations of interest in moneylending and related financial transactions.
The left column, labelled ‘F:6’ and ‘Dayes’, gives the simple interest at 6% on a capital sum of 1000000000 (109) over the number of days indicated by the middle column. The interest over a full year would be 6/100 × 109, so the interest over one day would be 6/365 × 107. The values are expressed decimally rather than in £.s.d and would need to be converted in use; the large number of significant figures gives sufficient precision for all ordinary calculations.
The rate of 6% was a standard one in England by the mid-17th century. The table is presumably titled ‘F:6’ because it indicates ‘forbearance’ at 6%. ‘Forbearance’ rather than ‘interest’ is used because there were continuing concerns about the religious probity of contracting for interest ahead of time. Though beginning to diminish in force in the 17th century, the Biblical injunctions against usury were still upheld by many. Forbearance was a way round the notion of usury, because the lender was foregoing the ability to profit from the sum that had been lent. (For more on the history of usury, see Norman Jones, God and the Moneylenders: Usury and Law in Early Modern England (Oxford, 1989).)
The right column, labelled ‘D:6’ and ‘Months’, is a table of discount, again at 6% interest. Each entry gives the discounted amount of money required to produce 10000000 (107) in the stated number of months at 6% interest. (Thus I only need to give you 9950249 if I owe you 10000000 in 1 month’s time.) If the value is x and n is the number of months, then the values are generated as follows:
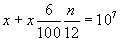
or, alternatively:
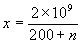
The particular format of the tables – their use of decimals and their brevity – is unusual and possibly unique. However, other contemporary tables of forbearance and discount can readily be found and it is clear that the intervals of days and months for forbearance and discount respectively were standard. In the preface to his Tabulæ Fœneratoriæ, or Tables for the Forbearance and Discompt of Money (London, 1653), Roger Clavell writes:
I have not here composed any other Tables of Forbearance of mony then for days to a year, or for any other then moneths for Discompt of money, since that dayes for the former is most exact ... and moneths for the latter is most concordant to the Merchants trade.
Clavell’s tables exclusively use a 6% interest rate ‘according to the late Act of Parliament’, and are tabulated using £.s.d. The tables are very extensive not just because they cover longer periods (up to a year for forbearance) but because they give values for different principal sums, from £10,000 down to 1 shilling.
Authorship
At present no definitive conclusions have been reached on the authorship of the content of this device. However, at least one intriguing possibility suggests itself.
The accountant and mathematical author, John Collins, wrote on simple and compound interest, annuities and related financial matters. In 1664/5 he issued a single folding sheet intended to be inserted in a letter case and to be used as a vade-mecum. This sheet carries the first 9 days of the simple interest table which appears on the silver oval. No instance of a similar discount table has yet been found in his work, but the notion of abbreviating the usually lengthy tables of interest into a portable form fits very nicely with the aide-memoire nature of the oval.
Collins was however not unique in expressing his work decimally rather than converting it back into £.s.d for public consumption. There was a flurry of interest in decimal arithmetic in mid-17th century England; see, for example, Charles Webster, The Great Instauration: Science, Medicine and Reform, 1626-1660 (London, 1975), pp. 414-5, 449. Webster also records wide-ranging decimal proposals such as Robert Wood’s 1656 manuscript tract ‘Ten to One, or a short and ready way for the extraordinary facilitation and dispatch of reckonings by means only of two or three new decimal coines much desired in order to the public good’ (Webster, p. 535-6). However, despite these contemporary concerns no other work has yet been found with the same tables as appear on the medallion.
Attribution
Aside from the author of the oval’s content, there is also the question of who actually made it. One avenue (perhaps the only realistic one) to pursue is via the engraving style.
At this stage, it is only possible to hazard a preliminary guess, based on a scan through 17th-century English instruments in the collection of the Museum of the History of Science, Oxford. However, it was noted that the unusual form of the ‘7’, with its curved descender, matches the work of the London mathematical instrument maker Hilkiah Bedford (working 1656 - 1680).
While further comparative research would be needed to substantiate this suggestion, it is worth noting that John Collins and Hilkiah Bedford were in contact and that Collins seems to have used Bedford as his mathematical instrument maker after the death of Henry Sutton in 1665. (On Bedford, see A. J. Turner, Time Museum, I: Time Measuring Instruments, Part 1: Astrolabes / Astrolabe Related Instruments (Rockford, 1985), p. 222, with references to the earlier literature.)
Conclusion
The information on this aide-memoire could have been recorded much more cheaply, and equally portably, on paper. Why does it exist as an engraved piece of silver, and what does it tell us about 17th-century English culture?
Firstly, it is not unique. It belongs to a small group of similar artefacts. For example, there is a silver example (41mm in diameter) of Sir Samuel Morland’s coin-calendar in the British Museum; see A. J. Turner, ‘A seventeenth century calendar scale for coins and mathematical instruments’, American Journal of Numismatics, second series, 5-6 (1993-94; published 1995), 209-219, p. 212. A contemporary aide-memoire for the mathematical art of fortification is closely analysed in D. J. Bryden, ‘The medal as a technical aide memoire: an example from Restoration England’, The Medal, 29 (1996), 139-47. There are also three surviving examples of a trigonometrical aide-memoire designed by the London mathematical practitioner John Sellar about 1681: two at the Whipple Museum, University of Cambridge (both brass) and one in silver sold at Sotheby’s London, 21 September 2000 (lot 35).
This group shows that there was a small but distinct genre of mathematical aide-memoires. Finely engraved on brass or silver they were presumably commissioned either by wealthy mathematical amateurs for their own use or perhaps by a practitioner as a gift for a potential patron. In any case, it only made sense to embody mathematics in this tangible form if there was a shared acceptance of the cultural value of the subject. The practical mathematical arts had clearly achieved recognition and esteem in the public sphere of later 17th-century England.
Acknowledgements
I first came across this object in 1997 as a public enquiry, passed on from a colleague. I deciphered the quadratic equations from a transcription of the engraving and subsequently saw photographs which confirmed the interpretation. I did not make any real progress with the numerical tables on the reverse. The object then resurfaced in 1998 when photographs of it were circulated as a ‘mystery object’ at a meeting of the Scientific Instrument Commission in Denmark. Rob van Gent (Utrecht) was able to show mathematically how the numbers were generated. This then led me to the 17th-century literature on interest. Further comments and suggestions have come from Frances Willmoth and Jackie Stedall.