
The mathematicians of the Renaissance applied their geometry to
all manner of practical disciplines - from navigation and surveying
to cartography, perspective and dialling. They aimed to demonstrate
the usefulness of geometry as well as its ingenuity and certainty,
and to associate it with action, achievement and progress. Many
new instruments were designed in this context, as the collections
of the Museum of the History of Science amply demonstrate.
Developments
in the art of warfare in the late fifteenth and sixteenth centuries
provided mathematicians with one such outlet for geometry. The
ability to make a heavy gun in a single metal casting led to ordnance
that was longer and capable of more accurate fire. Further, the
addition of trunnions on which the barrel could turn in a vertical
plane and the development of moveable carriages improved the setting
of direction and elevation, and so encouraged the idea of predicting
and calculating ranges. Practical mathematicians responded to
these changes by devising techniques, designing instruments and
writing books.
The speed with which the mathematicians responded
to the novel set of problems thrown up by changes in the conduct
of war is striking. It was in the sixteenth century that cannon
came to be used in large numbers and their effect became critical
to the outcome of military engagements; in the same period the
geometry of war became a major branch of practical mathematics.
To harness the capabilities of the new weaponry, gunners needed
instruments to measure both the inclination of the barrel and
the distance to the target, together with a means of relating
these two measurements; the geometers offered a variety of solutions,
as well as designs for fortifications to withstand attack from
the new artillery. The frequent wars in sixteenth-century Europe
added urgency to their work and helped justify claims for the
importance of their discipline. As in other areas of practice,
such as cartography or surveying, the mathematicians were quick
to recognize an opportunity and they responded with enthusiasm
- perhaps with over-enthusiasm, in view of the instruments and
images on view in this exhibition.
The ingenuity and precision
of the instruments on display, and the elegance, poise and delicacy
of many of them, contrast with the harsh and uncompromising conditions
of the battlefield. A review of such instruments is bound to raise
the question of how useful they could really have been in practice.
They were supposed to be employed in battle, but it is clear that
their purported military value also had other functions - in justifying
textbook geometrical problems, for example, and in attracting
patronage.
The exhibition at the Museum of the History of Science
seeks to draw attention to the fact that the advent, not of gunpowder
directly, but of its more effective use in improved ordnance,
precipitated a new variety of practical mathematics and a new
disciplinary discourse that flourished through the sixteenth and
seventeenth centuries. Though few historians of science or of
art have given it much attention, this geometrical discipline
engaged a great many practitioners in the period and was associated
with a range of technological developments applied throughout
Europe, both in military campaigns and in large works of military
engineering. The exhibition itself has three main sections, dealing
with gunnery, range-finding and surveying, and fortification.
The mathematics of troop formations is the first of two additional
topics, while the other is a reminder that the telescope - one
of the most emblematic instruments of science - was originally
introduced as an instrument of war.

The art of gunnery
was complex and dangerous and the gunner's ability to fire reliably
and accurately was frequently criticized. Although mathematicians
could not remedy variations in powder or in the form of individual
guns, they did seek to improve gunnery by devising instruments
for the measurement of shot, the elevation of guns and mortars,
and the calculation of the range of fire. Instruments for these
operations include calipers, gauges, quadrants, sights, levels
and specialized rules. Two or more of these elements were often
combined in a single design, in a marketing initiative typical
of mathematical instrument makers. Other mathematical instruments
such as sundials were also incorporated in the more exotic hybrids,
which typically date from the sixteenth or earlier seventeenth
centuries. By the eighteenth century, as mathematical instrument
makers became regular suppliers to professionalized ordnance departments,
more standard patterns were emerging.
Early modern gunners had
to cope with a bewildering variety of weaponry. Guns were named
according to their size, weight and length, or by the type and
weight of their shot. Each class of gun was different, and was
primed with specific amounts of powder (often inserted with individualized
ladles) before being loaded with its own shot. Printed sources
frequently tabulated the appropriate information for each type
of gun and some instruments likewise carry tables to serve as
aides-mémoire. Instruments were also enlisted to match
the correct size of shot to different guns. Calipers provided
measurements of the diameters of gun bores and of spherical shot,
and often directly indicated the weight of the shot. Gauging rods
also accomplished the same linking of diameter and weight, and
scales adapted for iron, lead and stone shot frequently appear
on German instruments.
Although heavy guns were often fired for
maximum destructive effect at point blank range (with the barrel
horizontal), greater range could be achieved by elevating the
gun. Quadrants, sights and levels enabled the gunner to set the
barrel at specified elevations. These instruments were constructed
in an enormous variety of forms and styles, with their scales
diversely graduated in degrees, inches or 'gunner's points'. In
his text of 1537 inaugurating the 'new science' of artillery,
Niccolò Tartaglia described a quadrant which was inserted
into the muzzle of the gun. Subsequent authors noted that this
exposed the gunner to enemy fire and they offered alternative
instruments which could be set up at the gun's breech. The many
surviving styles of levels and sights fall into this safer category
of instrument. Levels measure the inclination of the barrel using
a plumb line or a rigid plummet and a graduated arc. Sights have
a moveable pinhole or a series of fixed holes through which the
gunner observed, making an alignment with the top of the muzzle.
To
determine appropriate elevations for his cannons and mortars,
a gunner had to know the distance of the target and also be able
to relate this range to the elevation of the piece. The question
of determining the correct elevation necessary to fire a shot
a given distance (and its inverse, the prediction of range at
a given elevation) was the most taxing problem of gunnery as a
mathematical art. Gunners had their own rules of thumb, and instruments
were used to embody rules relating range and elevation. But questions
of ballistics also engaged the most prominent mathematicians.
Tartaglia set the terms of the debate by seeking to portray the
geometry of a projectile's trajectory based on the opposed natural
and violent motions of Aristotelian physics. His work provided
the basis for many subsequent accounts in textbooks and manuals.
Galileo offered a new foundation in his Discorsi of 1638, demonstrating
the parabolic path of projectiles and reinforcing the military
relevance of his work with a complete table of ranges. Through
the seventeenth and eighteenth centuries mathematicians of the
highest stature, such as Newton, sought more accurate depictions
of projectile trajectories by attempting to take into account
disturbing factors such as air resistance. Their sophisticated
efforts may have eluded the grasp of the average gunner, but do
demonstrate that the study of projectile motion was a point of
intersection for the art of war, the mathematical sciences and
contemporary natural philosophy.

How was the gunner
to determine the distance of his target? The traditional method
of linear measurement in land surveying was simply to lay ropes
or poles between the two stations concerned - hardly an option
when the distant station was a hostile position. However, sixteenth-century
geometers were seeking to introduce the technique of triangulation,
and range-finding was part of their case for a new geometry of
surveying. Distant stations could be located by sighting from
either end of a measured baseline; their distances were found
by measuring the angles formed with the baseline and by subsequent
calculation, or by a more straightforward graphical method. In
ordinary surveying, the possibility of triangulating as many features
as were required from a single linear measurement was presented
as an innovation that would greatly improve efficiency and convenience.
Range-finding offered a particularly appropriate application,
since access to the target feature was not simply inconvenient,
but impossible. Further it gave the designers of new surveying
instruments an immediate and telling example of the value of the
novel method, so that relevant instruments - particularly the
universal instruments, with all manner of claimed uses - were
frequently illustrated in dramatic and urgent action.
Two types
of surveying instrument were applied to triangulation and illustrated
in use in warfare. In the first group, comprising what are called
'triangulation instruments', parts of the instrument are arranged
to form a triangle similar to that on the ground, for example
by aligning rules with the lines of sight from the baseline. Scaled
measurements can then be taken directly from graduations on these
arms. The other category of instrument employs scales typically
found on the backs of astrolabes - the circular degree scale and
the shadow square or geometrical quadrant. This class includes,
of course, the astrolabe itself, but extends to the theodolite,
circumferentor and graphometer.
Such instruments were made relevant
to military life not only through the range-finding of the gunners.
It was claimed that they were generally helpful to the military
surveyor, either when laying out a new fortification, or when
measuring and representing an existing one. Accounts of the instruments
show them being used in such contexts and point to the particular
advantage of being able to survey from a safe distance.
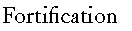

A
further relevant aspect of military surveying is the design of
fortifications. If guns precipitated new branches of the mathematical
sciences dealing with projectile motion and with range-finding,
they also created the conditions for a new military architecture.
Just as contemporary civil architecture was founded on geometry,
expressed through the classical style, so too the new genre of
fortification rested on a geometrical formalism.
The high walls
of the medieval fortress were good for repelling attack from beneath,
but were vulnerable to heavy guns: they presented large targets
without providing suitable platforms for defensive fire. Yet if
walls were to be low and stout, so as to withstand artillery bombardment,
how were they to be defended against direct infantry assault?
The new style of fortification emerged as a response to this problem.
The solution was to create squat, thick walls that were defended
by sidelong or flanking fire aimed from projecting gun emplacements
or bastions. These bastions had to offer protection to the adjoining
walls on either side and the whole fort had to be enclosed, resulting
in polygonal outline plans. The angled shape of the bastions was
progressively refined so that each bastion offered covering fire
to its neighbours and no 'dead space' remained hidden from defensive
fire. Beyond the primary wall and bastions, further positions
and defensive structures could be extended outwards. These limits
and rules set the conditions for the development of elaborate
geometrical designs, not always constrained by the features of
actual sites and the limited budgets of genuine commissions.
Such
celebrated practical geometers of the Renaissance as Francesco
di Giorgio, Filippo Brunelleschi, Leonardo da Vinci, Albrecht
Dürer and Simon Stevin were concerned with the solutions
to these problems, as were artists who might not be immediately
associated with a programme of this kind, such as Bramante and
Michelangelo. A species of practical geometry that began in Italy
in the later fifteenth century, spread to other parts of Europe
in the sixteenth, supported by the design of instruments and the
publication of books. The general recommendation was for arrow-headed
bastions projecting from the corners of a walled polygon, but
beyond this there was plenty of scope for individual styles and
schools. In practice the basic polygon often had to accommodate
the natural conditions of the site or its existing structures.
The French school took the lead in the development of such systems
in the second half of the seventeenth century, with the practice
and theory of Sébastien le Prestre de Vauban dominant into
the eighteenth. The outcome was a vast programme of work and a
thriving specialist geometrical discipline.
Geometers had to consider
not only the plan of an ideal fortification: the section offered
them further possibilities. Fortress defenders wanted both to
impede the progress of any attackers and to oblige them to present
an advantageous target for their guns. A large ditch in front
of the rampart was fundamental to defence, and the earth from
the ditch provided an embankment on the outer border that both
obscured the walls and provided a sloping approach, angled so
as to be swept by defensive fire. Other features could be incorporated,
such as the covered way on the outer side of the ditch, for patrols
shielded from fire. As with the plan or 'trace', the result was
an elaborate structure subject to revision and adjustment by different
practitioners.

As a new branch
of mathematical science, the geometry of war was ambiguously positioned
in a number of respects and these ambiguities deserve attention
from historians. Was this a practical science or a polite one?
Did it belong at war or at court? Was it driven by practice or
by theory? Was it characterized by action or by rhetoric? Was
it part of mathematics or of natural philosophy? Answers to each
of these questions fall somewhere between the two respective alternatives,
and their positions on each of these ranges of possibilities change
over time. It is within these ambiguities and changes that some
of the most interesting aspects of the subject are to be found.
The
tension between the practical and the polite is perhaps most obvious
in the contemporary literature. Instruments are illustrated in
use where conflict is imminent or already begun, and the coolness
of the practitioners who apply their geometry in the heat of battle
can seem improbable. Such examples of purported use initially
served to stress the potential importance of the practitioners'
geometrical techniques. With the acceptance that aspects of warfare
were amenable to geometry, the association could be used to justify
a group of mathematical problems that in practice would remain
confined, for the great majority of readers, to textbook instruction.

The
same can be observed in the progress of popular interest in fortification.
Both gunnery and fortification become established in general encyclopaedic
works aimed at the gentle market, and polygonal scales are included
in a conventional way on a variety of instruments whose links
to professional military surveying seem implausible. By the end
of the period covered by the exhibition, popular lecturers in
eighteenth-century London, such as Benjamin Martin and Erasmus
King, were offering fortification as mathematical entertainment.
Another lecturer, W. Griffiss, tackled the subject in a tavern
in the evening, 'illustrated by various Plans, and a large Model
of a fortified Town', and repeated the performance the following
morning 'for the better Accommodation of the Ladies' (Morton & Wess, p. 73).
Military mathematics likewise featured in academic
as well as coffee house teaching. To take a local example, David
Gregory proposed a new mathematics course for Oxford in 1700 which
included 'a lecture on fortification, so far as 'tis necessary
for understanding it without actually serving in an army or forttifying
a town or camp' (quoted in Bryden). The museum building itself
witnessed instruction in fortification in the very room where
the present exhibition has been mounted, when John Whiteside introduced
the subject into his course on mathematics in 1723. At the same
time as these popular and academic activities, there was at the
practical level an active programme of fortress construction across
Europe, and this lent credibility and status to the polite interest.
It
is probably the surviving instruments that most eloquently address
the tension between the courtly context and the battlefield. Elegant
and ingenious instruments, perhaps in gilt brass and accompanied
by tooled leather cases, were far beyond the material and probably
the educational resources of the ordinary gunner. They could,
however, enhance the image of an active officer abreast of the
finer points of contemporary warfare. The maker offered a rare
accessory to enhance a courtly posture and in exchange the patron
offered a valuable and perhaps prominent commission. Instrument
design might itself accommodate a rhetorical or gestural aspect,
as when mathematical instruments are made to resemble, or even
to act as, weapons. Yet not all surviving instruments fall into
this class: they range from the improbably ornate to the crude
and humble, and we must remember that the former are much more
likely to have found their way into museum collections. We know,
for example, that the British Board of Ordnance ordered gunner's
quadrants and perpendiculars in quantity. On the other hand again,
John Muller, Professor of Fortification and Artillery at the Royal
Military Academy, Woolwich, says that gunners should learn to
judge by eye and dismisses the use of instruments in his Treatise
of Artillery of 1757.

The geometry of war sits ambiguously too
between practice and theory. It is an ambiguity characteristic
of the mathematical sciences and one from which they derived their
potential for influential development in the Renaissance. Leonard
Digges points clearly to this in his Pantometria of 1571, where
he asserts that the perfection of gunnery is beyond both the mathematical
novice, 'though hee turmoile in powder and shot all the dayes
of his life', and equally the geometer, 'leaning onely to discourse
of reason', who 'shall fall into manifolde errors, or inextricable
Laberinthes.'The tension between deeds and words, between action
and rhetoric, is particularly evident in contributions from the
practitioners themselves, or at least from writers who present
themselves as practitioners. Robert Norton, who describes himself
as 'one of his Maiesties Gunners and Enginiers' on the title-page
of The Gunner of 1628, asserts firmly that '… lead on by
Experience the Mistris of all Arts, Action being the best Tutor
… I … haue endeuoured herein more to respect a few experimented
truthes, then many Rhethoricall imbellishments of words.' An 'experiment'
at the time has the sense of a deed or venture, as distinct from
a discussion or projection, without the more specific reference
it came to have in later science. But it is clear that the sentiment
of the Royal Society's motto, 'nullius in verba', had an earlier
currency in this empirical tradition.
Finally there is the changing
position of gunnery between mathematical science and natural philosophy.
The former of these separate branches of Renaissance learning
dealt with mathematics and its practical applications, while the
latter was concerned with causal explanations of natural phenomena.
Norton again was bullish and provocative: gunnery, he said, was
a profound study, 'euen able to spose the knowne parts of Naturall
Philosophy, Arithmetick, Geometry, and Perspectiue, each of which
her handmayd is'. In reality the relationship was much more ambiguous,
but the fact that this aspect of practical geometry raised questions
pertinent to natural philosophy may be relevant to the emergence
of a new relationship between the two - one where mathematics,
experiment and instruments are all recruited to a reformed explanatory
programme for the natural world.
The exhibition concludes with
one such connection. Galileo began his career as a mathematical
scientist, a teacher of practical mathematics, including fortification,
and a designer of mathematical instruments. His ambitions, however,
were towards the higher science of natural philosophy and one
instrument he was involved with - the telescope - though it began
as an instrument of warfare, became in his hands a reforming tool
of natural philosophy. Reform was foreshadowed in two ways - through
the telescopic observations Galileo marshalled in support of Copernicus,
and through his use of an instrument as a means of investigating
the natural world.
The telescope was a new departure in the methodology
of natural philosophy, but it was through projectile motion that
the discipline was most directly implicated in the geometry of
war. Early writers on ballistics - Tartaglia and his successors
- couch their discussions in terms of the natural and violent
motions of Aristotelian physics. The form of the ballistic trajectory,
traced by an initially rising projectile which then begins to
falter and to descend, was presented as the combined outcome of
the two opposed motions and the transition between them. The superiority
of Galileo's technical achievement in the Discorsi should not
blind us to the significance of a century of problem setting and
the significance too of setting the terms of a solution - that
is, as a geometrical trajectory with universal reference yielding
predictable consequences. The treatment from Tartaglia onwards
is thus characteristic of the mathematical sciences and particularly
of their most sophisticated branch, astronomy.
Although Newton's
success in Principia is often presented as a transcendent achievement
of the geometry of reason, part of the prior development that
made 'the mathematical principles of natural philosophy' a viable
conjunction was contained in the geometry of war. Almost two hundred
years after the Renaissance discourse of ballistics was opened
by Tartaglia, Newton, in his System of the World (published posthumously
in 1728), explained the dynamics of planetary motion in terms
of a body projected horizontally from a mountain top with successively
greater initial velocity. The problem is the old one of point-blank
range but, not only has Newton escaped from the language of gunnery
into that of abstract mechanics, the range of his projectile extends
until, instead of descending to earth, it falls forever in an
orbital trajectory.

Exhibition Contents Introduction Summaries
Essay Catalogue Figures Bibliography Name Index
Museum Home Page